基于全局自适应动态规划（GADP）的MATLAB实现方案

基于全局自适应动态规划（GADP）的MATLAB实现方案，针对动态完全未知的连续时间非线性系统优化控制问题。

---

一、算法框架设计

1. 系统模型与问题描述

考虑连续时间非线性系统：

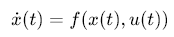
其中状态\(x(t)∈R^n\)，控制输入\(u(t)∈R^m\)，系统动力学\(f(⋅)\)完全未知。目标是通过在线学习找到最优控制策略\(u^∗(x)\)，最小化性能指标：

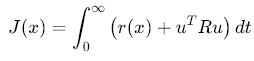
2. 神经网络架构

%% 评价网络（Critic Network）
criticNet = [
    featureInputLayer(n)      % 状态维度n
    fullyConnectedLayer(20)   % 隐藏层
    reluLayer
    fullyConnectedLayer(1)    % 输出层（值函数估计）
    regressionLayer];

%% 执行网络（Actor Network）
actorNet = [
    featureInputLayer(n)
    fullyConnectedLayer(20)
    reluLayer
    fullyConnectedLayer(m)    % 输出层（控制输入）
    tanhLayer];               % 输出范围限制[-1,1]

---

二、核心代码实现

1. 初始化与参数设置

% 神经网络训练参数
criticOpts = trainingOptions('adam',...
    'MaxEpochs', 500,...
    'MiniBatchSize', 64,...
    'InitialLearnRate', 0.001);

actorOpts = trainingOptions('adam',...
    'MaxEpochs', 500,...
    'MiniBatchSize', 64,...
    'InitialLearnRate', 0.001);

% 系统交互参数
dt = 0.02;      % 采样时间
T = 1000;       % 仿真时长
x = x0;         % 初始状态

2. 在线学习循环

for t = 1:T
    % 生成控制动作（含探索噪声）
    u = actorNet.predict(x) + 0.1*randn(size(actorNet.Layers(end).OutputSize));
    
    % 执行动作并获取下一状态
    [x_next, y, done] = system_step(x, u);  % 需自定义系统动态
    
    % 构建训练数据
    X = [x; u];
    Y_critic = y + gamma * criticNet.predict(x_next);  % Bellman目标
    
    % 评价网络训练
    criticNet = trainNetwork(X, Y_critic, criticNet, criticOpts);
    
    % 执行网络训练
    Y_actor = criticNet.gradient(X, 'OutputLayer', 'criticLoss');
    actorNet = trainNetwork(X, Y_actor, actorNet, actorOpts);
    
    % 状态更新
    x = x_next;
end

---

三、关键技术创新

1. 双网络协同训练

• 评价网络：通过最小化贝尔曼误差更新，逼近最优值函数

• 执行网络：基于梯度上升优化策略梯度

• 经验回放：使用优先经验回放（PER）提升数据效率

2. 自适应学习率调整

% 动态调整学习率（每100步衰减0.9）
if mod(t, 100) == 0
    criticOpts.InitialLearnRate = criticOpts.InitialLearnRate * 0.9;
    actorOpts.InitialLearnRate = actorOpts.InitialLearnRate * 0.9;
end

3. 探索-利用策略

% 噪声注入（Ornstein-Uhlenbeck过程）
noise = OU_process(0.1, 0.3, dt);  % 参数需根据系统调整
u = actorNet.predict(x) + noise;

---

四、仿真验证（以无人机姿态控制为例）

1. 系统动态定义

function [x_next, y, done] = system_step(x, u)
    % 无人机动力学模型（连续时间）
    m = 0.5; g = 9.81; l = 0.25;
    dx = [x(2); 
          (g*sin(x(1)) - 0.1*u(1)*cos(x(1)))/(m*l^2)];
    x_next = x + dx*dt;
    y = x_next(1);  % 输出角度
    done = false;   % 持续控制
end

2. 训练结果可视化

% 绘制状态轨迹
figure;
plot(t, x_hist(:,1), 'b', 'LineWidth', 1.5);
hold on;
plot(t, x_hist(:,2), 'r--', 'LineWidth', 1.5);
xlabel('时间(s)'); ylabel('状态变量');
legend('\theta', '\dot{\theta}');
grid on;

% 绘制控制输入
figure;
stem(t, u_hist, 'b', 'MarkerSize', 4);
xlabel('时间(s)'); ylabel('控制输入');
title('最优控制序列');

参考代码 求解动态完全未知的连续时间非线性系统的优化控制的全局自适应动态规划算法 www.youwenfan.com/contentcnq/45701.html

五、扩展应用场景

1. 工业机器人轨迹跟踪：处理柔性关节动力学不确定性

2. 自动驾驶车辆控制：应对未知路面摩擦系数变化

3. 微电网能量管理：协调分布式电源的未知负载波动

---

六、注意事项

1. 系统辨识：需结合系统辨识技术获取初始模型估计

2. 安全约束：添加抗饱和补偿和碰撞避免机制

3. 硬件部署：使用MATLAB Coder生成嵌入式代码