练习：回家（选票定理Ballot Theorem）

点击查看题目

内存限制：128 MiB

时间限制：1000 ms

标准输入输出

题目类型：传统

评测方式：文本比较

题目描述

小Z是个路痴。有一天小Z迷路了，此时小Z到家有 n 个单位长度。小Z可以进行若干次行动，每次行动小Z有 \(\frac 1 2\) 的概率向家靠近一个单位长度，有 \(\frac 1 2\) 的概率向家远离一个单位长度。由于小Z的体力是有限的，他最多能行动 k 次。请你帮帮可怜的小Z算一算，他在体力耗尽之前到达家中的概率是多少。

输入格式

一行两个用空格分隔的整数 n,k 。表示小 Z 到家的距离和小 Z 能行动的次数。

输出格式

一行一个整数表示小 Z 回到家的概率，结果对 998244353 取模。

样例

样例1输入

1 3

样例1输出

374341633

样例2输入

5 10

样例2输出

889061377

样例3输入

2400 5000

样例3输出

669056278

样例4输入

3123456 4987654

样例4输出

139700926

容易想到首先可以枚举经过了多少步到达位置 \(n\)。

假设目前走了 \(i\) 步，那么其中肯定走了 \(\frac {n+i}{2}\) 步是向家走的，有 \(\frac {i-n}{2}\) 步不是向家走的。

那么到达家的总方案数为 \(C_{i}^{\frac {n+i}{2}}\)。

现在需要排除掉提前走到了目标位置的情况。

这时候就需要用到 Ballot Theorem 选票定理了。

根据选票原理，我们就能得到这些方案中有 \(\frac{n}{i}\) 是第一次到达的情况。

证明如下：

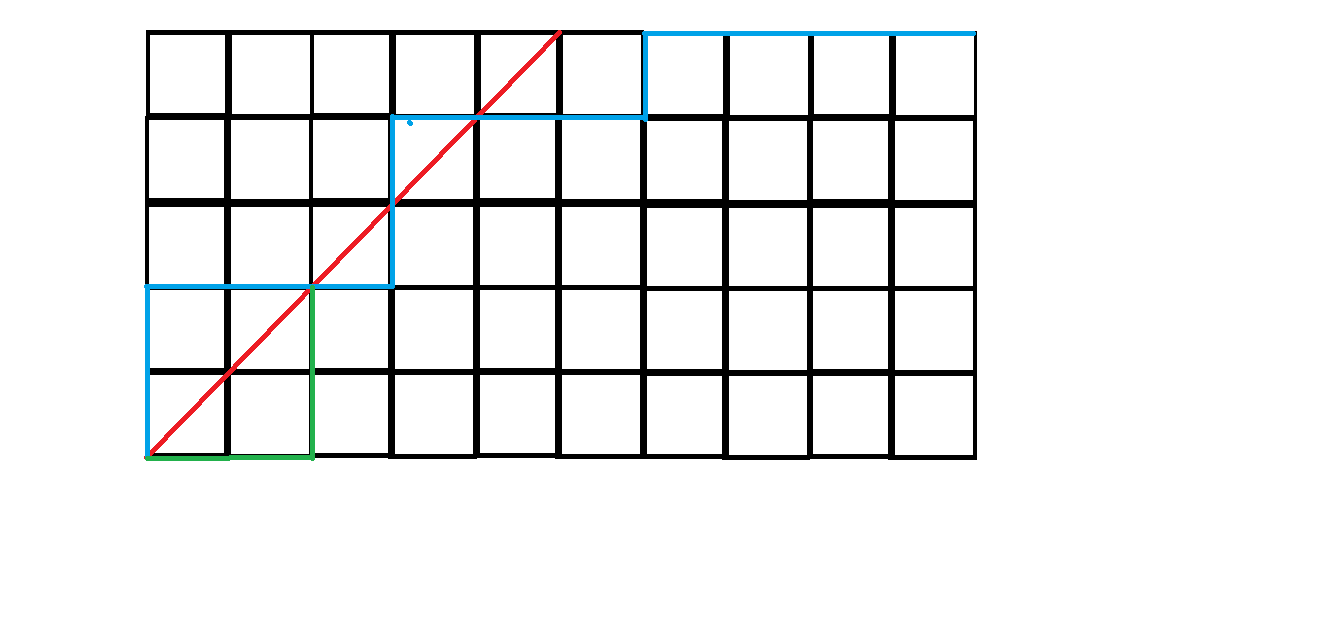
我们将问题转化为二维平面上的问题，要求除开始外不能经过中间这条线。

由于反过来做方案数是一样的，我们就可以要求每一步向上或者向右，最后到达一个向右距离大于向上的位置，对应题目中的关系。

那么我们可以发现，对于一个不满足条件的情况，可以将从开始一直到这条线的部分翻转过来，就会唯一对应一个开始时直接向上的不可能满足条件的情况。

并且可以发现每一个开始时向上最后到达终点位置的情况一定也有唯一对应的，因为肯定要重新过这条线。

那么就可以得到一开始向上走的情况与一开始向右走且不满足情况的方案数相等。

不难发现这里向上走就相当于原题目最后一步是远离家的方向的情况，那么概率就是 \(\frac{i-n}{2i}\)。

合法状态就是直接容斥，只有上面两种不满足的情况，直接计算：\(1-2\times \frac{i-n}{2i}=\frac{n}{i}\) 即为合法概率。

就证好啦。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=998244353;
int ans,n,k,fac[5000005],inv[5000005],pw[5000005];
int ksm(int a,int b){
	int s=1,x=a;
	while(b){
		if(b&1)s=s*x%mod;
		x=x*x%mod;
		b>>=1;
	}
	return s;
}
int C(int x,int y){
	return fac[x]*inv[y]%mod*inv[x-y]%mod;
}
signed main(){
	fac[0]=pw[0]=1;
	for(int i=1;i<=5000000;i++)fac[i]=fac[i-1]*i%mod,pw[i]=pw[i-1]*499122177%mod;
	inv[5000000]=ksm(fac[5000000],mod-2);
	for(int i=5000000;i>=1;i--)inv[i-1]=inv[i]*i%mod;
	cin>>n>>k;
	for(int i=n;i<=k;i+=2){
		ans=(ans+n*ksm(i,mod-2)%mod*C(i,(i+n)>>1)%mod*pw[i]%mod)%mod;
	}
	cout<<ans;
	return 0;
}