Educational Codeforces Round 185 (Rated for Div. 2)

Dashboard - Educational Codeforces Round 185 (Rated for Div. 2) - Codeforces

贪心合集

B

题目要求我们要选择一个最长的+1区间来构成B数列

所以B的顺序没什么意义，所以先从大到小排序

然后可以观察到样例1

5 1 1 0 0 这个一共就有三个有效数字，所以最长也是3

然后我们进行5次是在一个区间内-1，把这个5 1 1弄成0 0 0，问最长的区间是多长

5 1 1 -> 4 1 1 ->3 1 1 -> 2 1 1 ->1 1 1-> 0 0 0

也就是当前这个5 1 1处理5次的话可以余下一个 1 1 1的整个序列进行一次最长为3的操作

还是5 1 1 我们操作6次呢

5 1 1 -> 4 1 1 ->3 1 1 -> 2 1 1 ->1 1 1-> 到了现在，   1 1 1 我们现在余下2次操作最优的是有一个1单独出来，剩下的一组 

7次操作同理我们到达 1 1 1时还有3次操作，执行分段 1 ， 1， 1一个一段，答案就是1

所以我们得到一个小结论，把数组简化为全1的数组的同时当前的K操作越小越好，越小答案越大

那如何让余下的操作最小呢，就是在处理到全1的过程中尽可能地浪费次数，我非要l==r的进行操作

也就得到了我们拼尽全力去浪费的话，浪费的次数应该是     所以如果浪费的次数>=（n-1）的话，

我们总是可以余下一次操作然后把1 1 1 1 1……全部一下剪掉

void solve(){
    int n;cin>>n;
    vector<int>sh(n);
    for(auto &it:sh)cin>>it;
    sort(all(sh),greater<int>());
    int res=n,ans=0;
    for(auto it:sh){
        if(it<=1)break;
        res-=it-1;
    }
    for(int it:sh){
        if(!it)break;
        ans++;
    }
    ans-=max(0ll,res-1);
    cout<<ans<<endl;
    return ;
}

C

需要进行一个简单的数学计算，

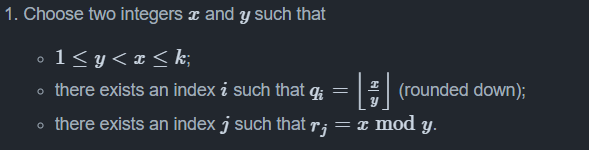
 对于单个qi，ri来说一定存在一对x，y满足下面两个要求，但只是有个<=k的约束，先考虑没有条件一

qi为x时y的倍数，rj是x对y的取余数，有倍数有余数就可以求关系   qi*y+rj=x 

我们要尽可能的保证x和y最小的话，需要模数y最小，当且仅当y=rj+1的时候y和x都是最小的，也就是如果这一对数满足可以满足<=k的话，那就说明可以操作qi，rj

这存在一个单调关系，如果qi可以与rj进行操作的话，那比rj小的r都可以满足；同理，如果比qi小的也可以与rj进行操作

所以这就涉及到一个双指针，意味着我们只要当前最极限的两个数进行配对，以至于不会造成浪费，我们用qi配对当前可以满足的最大的r

如果存在这个r就说明qi可以去掉，如果没有任何一个r满足，就说明从当前的qi开始往后大于qi的所有数字都找不到适配的r来操作

当r完全用完的时候，就是最大匹配

void solve(){
    int n,k;cin>>n>>k;
    vector<int>q(n),r(n);
    for(auto &it:q)cin>>it;
    for(auto &it:r)cin>>it;
    sort(all(q));sort(all(r));
    int qt=0,rt=n-1,ans=0;
    while(qt<n&&rt>=0){
        if(r[rt]>=k){
            rt--;continue;
        }
        int y=r[rt]+1;
        int x=q[qt]*y+y-1;
        if(x>k){
            rt--;
            continue;
        }
        qt++;
        rt--;
        ans++;
    }
    cout<<ans<<endl;
    return ;
}

D（待补）

一个构造题目，好像也是贪心，马上补