初学多项式与生成函数笔记 Part I
参考文献
算法学习笔记(6):指数生成函数(EGF)- GhostLX
一、快速傅里叶变换 FFT
1. 多项式引入
先要知道多项式的定义是啥,其实跟七上学的一样,形式化就记为:
而在这里面,其实我们并不会将 \(x\) 真的看作一个未知数,我们会把它看作一个形式符号。此时多项式实际上表示的就是一个序列,记作 \(f=\lang f_0,f_1,f_2,\cdots,f_n \rang\)。
有穷项的求和,我们将其称作多项式,无穷项呢?我们将其称作形式幂级数。
多项式的加法减法,无疑是明显的,各次数相加即可。而最核心的是两个多项式乘法。
若有多项式 \(f(x),g(x)\),它们的积为 \(Q(x)=f(x)\cdot g(x)\),则有。
这是很好理解的。问题在于,我们要如何计算这个东西呢?朴素做法是 \(O(n^2)\) 的,很不好,于是这就是多项式中最基础的一个算法——快速傅里叶变换。
2. 多项式的点值表达
我们现在把一个多项式看作一个函数。
那么由初中知识就可以知道,我们用待定系数法,知道 \(2\) 个点的坐标就可以确定一个一次函数,知道 \(3\) 个不共线的点就可以确定一条抛物线……以此类推,知道 \(n+1\) 个点的坐标就可以确定一个(至多)\(n\) 次函数。
因此我们可以用 \(n+1\) 个点值来描述一个多项式,这个就叫做点值表达。这个有什么好处呢?
例如对于两个 \(n\) 项多项式 \(F(x),G(x)\),现在要求 \(Q(x)\),怎么办?我们可以绕一下路。先将 \(F(x)\) 和 \(G(x)\) 两者的一组 \(x\) 相同的点值表达弄出来,然后将它们一一相乘,得出的数列,你会发现,这就是 \(Q(x)\) 的点值表达,于是就可以确定 \(Q(x)\) 了。
现在的问题就在于,如何快速在多项式的系数和点值间转化呢?有高斯消元 \(O(n^3)\),拉格朗日插值 \(O(n^2)\),但还不够。会发现在多项式的乘法中,点值是由我们自己选,因此,我们考虑一组,有很好的性质的点值。
3. 复数与单位根
我们知道虚数单位,也就是 \(\text{i}^2=1\)。于是自然的,我们引入复数,\(z=a+b\text{i}\)。
在实数的时候,对于每一个 \(x\in\text R\),在数轴上,都有唯一确定的点与之对应,且互不相同。而在虚数这里,可以看到,一个一维的东西就不够了。于是我们把它放到一个平面上,就叫复平面。因此复平面上的每一个点,都唯一对应了互不相同的复数。
不仅如此,若这个点为 \(Z(a,b)\),那么这个复数还唯一对应了一个平面向量 \(\vec{OZ}\)。
复数的加减法和乘法是显然的,不多阐述。
定义一个复数 \(z=a+b\text i\) 的模为对应向量的长度,\(\sqrt{a^2+b^2}\)
定义一个复数 \(z=a+b\text i\) 的辐角为 \(\theta\),其中 \(\tan \theta =\dfrac b a\)。
而在此时复数的乘法就非常干脆了:复数乘法,辐角相加,模相乘。
这里,我们引入欧拉公式:
记住这个公式,只需要记住把 \(\text i\) 乘在 \(\sin\) 上即可。
这玩意有什么用呢?你考虑这样一个复数 \(z=a+b\text i\)。
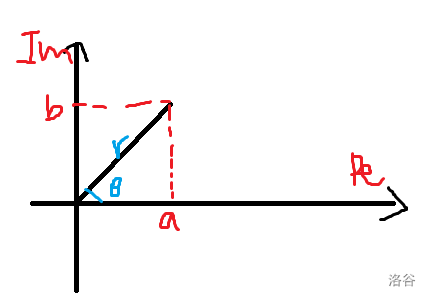
你会发现,\(a=r\cos\theta,b=r\sin\theta\),因此就有 \(z=a+b\text i=r(\cos\theta+\text i\sin\theta)\)。
欸,那后面不就是欧拉公式的形式了吗?替换一下:\(z=r\text e^{\text i\theta}=r\exp (\text i \theta)\)。(\(\exp x\) 是 \(\text e^x\) 的一种简写)
我们考虑这个方程:\(x^n=1\),首先你会发现在实数底下只有 \(x_0=1\),哦我的天哪。
放到复数来,\(1\) 对应的就是 \(x\) 正半轴的那个位置。现在相当于问你有哪些 \(r=1\) 的向量,转 \(n\) 次刚好转到 \(x\) 正半轴来。显然,\(\theta=\dfrac{2\pi}n\) 是一个,因此,\(2\theta,3\theta,\dots,(n-1)\theta\) 的角度都是可以的。
因此,我们设 \(r=1,\theta=\dfrac{2\pi}{n}\) 的复数叫做 \(n\) 次单位根,即 \(\omega_n=\exp\dfrac{2\pi}{n}\)。
4. 离散傅里叶变换
那么我们刚才说想要的那一组特殊的点值,其实就是 \((\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1})\)。
于是现在我们要干的事情,就是如何快速的求出这些点值呢?我们形式化一下我们的问题,即求一个长 \(n\) 的数列 \(\bf b\),有。
我们称,\(\bf b\) 为 \(\bf a\) 的离散傅里叶变换,即 DFT。
以下设 \(n=2m\)。
我们现在考虑把多项式 \(A(x)\) 的项,按奇偶分类。
看上去很何意味,但是这就相当于,我们把这个问题分治了。若定义
则求 \(x\) 的点值就分治成了,求 \(A_0\) 与 \(A_1\) 在 \(x^2\) 上的点值了,即 \(A(x)=A_0(x^2)+xA_1(x^2)\)。
那假如说我们现在求一个具体的,例如 \(\omega_n^k\) 的点值,就有:
为什么 \(\omega_n^{2k}=\omega_m^k\)?放在单位圆上就好理解了。
同理,还有
这两部就是 FFT 的精髓,蝴蝶操作。
这意味着什么?如果我们得到了多项式 \(A_0,A_1\) 在点 \(\omega_m^0,\omega_m^1,\dots,\omega_m^{m-1}\) 的点值的话,我们可以直接 \(O(n)\) 合并得到 \(A\) 在 \(\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1}\) 的点值!
分析一下时间复杂度。由于递归树每一层都是线性的,因此整体就是 \(O(n\log n)\) 的。哦耶。
5. 递归转迭代与 IDFT
我们分组下去,是将二进制拆分后,最后一位为关键字,然后倒数第二位……一直到最高位。
因此你会发现,如果我们把二进制逆序,归并的顺序恰好就是 1,2,3,…,N。
对于 DFT:
有逆变换 IDFT:
6. 实现
对于 IDFT,你会发现 \(a_k\) 的答案,对应了正常 DFT \(n-k\) 的答案,因此最后进行 IDFT 时直接将数组逆序即可。
const int N=6e6+10;
const double PI=acos(-1); //利用 arccos 获取 pi 值
int rev[N]; //预处理二进制逆序的值
void get_rev(int n){
int d=n>>1,cur=0; //d -> 当前放置到哪一位了
rev[cur++]=0,rev[cur++]=d;
for(int w=2;w<=n;w<<=1){
d>>=1;
for(int p=0;p<w;p++) rev[cur++]=rev[p]|d;
}
}
complex<double> F[N],G[N]; //stl 复数类
//FFT 算出来对应的点值直接覆盖在系数数组 A 上
void FFT(complex<double> *A,int n){
for(int i=0;i<=n;i++) if(rev[i]>i) swap(A[i],A[rev[i]]);
// 一个快捷的排序算法,你会发现 rev[rev[i]]=i
// 那么对于新序列中,交换仅限于 i 和 rev[i] 这一对下标对应的数中
for(int len=2,m=1;len<=n;m<<=1,len<<=1){
// len 表示当前合并的长度
complex<double> W(cos(PI/m),sin(PI/m)),I(1.0,0.0); //W -> n 次单位根
for(int L=0,R=len-1;R<=n;L+=len,R+=len){
complex<double> w0=I;
for(int p=L;p<L+m;p++){
complex<double> x=A[p]+w0*A[p+m];
complex<double> y=A[p]-w0*A[p+m];
A[p]=x,A[p+m]=y;
w0*=W;
//正常蝴蝶操作
}
}
}
}
int n,m,k,sum;
//由于 FFT 是分治的,我们要将 sum=n+m 自动向上到第一个二的幂 k
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
sum=n+m,k=1;
while(k<=sum) k<<=1;
get_rev(k);
for(int i=0;i<=n;i++){
int tmp; cin>>tmp;
F[i]=tmp;
}
for(int i=0;i<=m;i++){
int tmp; cin>>tmp;
G[i]=tmp;
}
FFT(F,k);
FFT(G,k);
//算点值
for(int i=0;i<k;i++) F[i]*=G[i];
FFT(F,k);
reverse(F+1,F+k);
//注意到 1 次对应的应该是 k-1 次
for(int i=0;i<=sum;i++) cout<<int(F[i].real()/k+0.5)<<" ";
cout<<"\n";
return 0;
}
二、快速数论变换 FNTT
NTT 是 DFT 在数论上的实现,而 FNTT,则为 FFT 在数论基础上的实现。当然,一般提到 NTT,都指的是快速数论变换。
这里并不是很有闲心写那些神秘定义,数论好无聊啊,直接给出一些映射:
- 自然底数 \(e\) 对应模数 \(p\) 的原根 \(g\)。
- 一圈 \(2\pi\) 对应 \(p-1\)。
- 因此 \(n\) 次单位根 \(\omega_n\equiv g^{\frac{p-1}n}\pmod p\)。
你会发现为了方便,我们要找有如下性质的质数:
- 有原根
- 减掉一,刚好是某个 \(2\) 的次幂的倍数
\(998244353\) 就是个不错的选择,其等于 \(7\times17\times2^{23}+1\),原根为 \(3\)。
好,剩下的完全一样,来个板子。
const ll N=6e6+10;
const ll P=998244353,g=3;
//模数 原根
ll rev[N];
void get_rev(ll n){
ll d=n>>1,cur=0;
rev[cur++]=0,rev[cur++]=d;
for(ll w=2;w<=n;w<<=1){
d>>=1;
for(ll p=0;p<w;p++) rev[cur++]=rev[p]|d;
}
}
ll qpow(ll a,ll k){
ll res=1;
while(k){
if(k&1) res=res*a%P;
a=a*a%P,k>>=1;
}
return res;
}
ll F[N],G[N];
void NTT(ll *A,ll n){
for(ll i=0;i<=n;i++) if(rev[i]>i) swap(A[i],A[rev[i]]);
for(ll len=2,m=1;len<=n;len<<=1,m<<=1){
ll W=qpow(g,(P-1)/len);
for(ll L=0,R=len-1;R<=n;L+=len,R+=len){
ll w0=1;
for(ll cur=L;cur<L+m;cur++){
ll x=(A[cur]+w0*A[cur+m]%P)%P;
ll y=(A[cur]-w0*A[cur+m]%P+P)%P;
A[cur]=x,A[cur+m]=y;
w0=w0*W%P;
}
}
}
}
ll n,m,sum,k;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>m;
sum=n+m,k=1;
while(k<=sum) k<<=1;
get_rev(k);
for(ll i=0;i<=n;i++) cin>>F[i];
for(ll i=0;i<=m;i++) cin>>G[i];
NTT(F,k),NTT(G,k);
for(ll i=0;i<k;i++) F[i]=F[i]*G[i]%P;
NTT(F,k);
reverse(F+1,F+k);
ll invk=qpow(k,P-2);
for(ll i=0;i<=sum;i++) cout<<F[i]*invk%P<<" ";
cout<<"\n";
return 0;
}
三、生成函数初步
1. 形式幂级数引入
级数,就是列项相加的求和式。有正向级数,交错级数,幂级数等等等等。
而这里我们研究幂级数,它的每项均为非负整数次幂乘上一个常数系数,即
换一个话题,我们之前已经引入多项式的定义了,假如我们允许无穷项的存在,即
我们就称其为形式幂级数。之所以在这之前加上形式二字,是因为我们用这个式子常常是用于多项式的计算中,\(x\) 只是一个形式符号,许多级数相关的东西我们完全不去理会,因此就叫做形式上的幂级数。
形式幂级数的加减法是正常的,即
对于乘法运算,其就是卷积
哦对了,为方便,称 \(F(x)\) 第 \(n\) 项的系数为 \([x^n]F(x)\)。
2. OGF 的定义和用处
于是我们称一个序列 \(a\) 的普通生成函数(ordinary generating function,OGF)定义为形式幂级数
比如说,序列 \(a=\lang1,2,3\rang\) 对应的 OGF 是 \(1+2x+3x^2\),这是有限项的例子;再比如说序列 \(a=\lang1,3,5,7,9,\dots,\rang\),其 OGF 是 \(\sum\limits_{n\ge 0}(2n+1)x^n\),这是无限项的例子。
换言之,一个普通生成函数的系数,其实就是序列 \(a\) 对应的通项公式。
这玩意有啥用,不妨举个例子。
现在有 \(3\) 枚 \(A\) 硬币,\(2\) 枚 \(B\) 硬币,\(4\) 枚 \(C\) 硬币,凑出 \(n\) 枚硬币有多少种方式?
对于一类硬币,我们定义一个序列,其中第 \(i\) 项表示 \(i\) 枚此种硬币能否被取到,例如:
\(a=\lang1,1,1,1,0,0\dots\rang\)
\(b=\lang1,1,1,0,0,\dots\rang\)
\(c=\lang1,1,1,1,1,0,0,\dots,\rang\)
因此,它们对应的生成函数分别是:
\(A(x)=1+x+x^2+x^3\)
\(B(x)=1+x+x^2\)
\(C(x)=1+x+x^2+x^3+x^4\)
你把它们乘起来得到的东西,即 \(A(x)B(x)C(x)\),你会发现它的第 \(n\) 项系数正等于凑出 \(n\) 枚硬币的方案数!这是为啥呢?
感性地,你把 \(x^1\) 看成一枚硬币,\(x^n\) 代表 \(n\) 枚硬币。你会发现 \(x^1\cdot x^3=x^4\),代表的实际意义就是 \(1\) 枚硬币加上 \(3\) 枚硬币等于 \(4\) 枚硬币。因此多项式乘法,在每一个因式里面挑一项相乘,实质上就是在尝试所有的选择路径。而 \(x^n\) 的系数,就是 \(x^0\) 到 \(x^n\) 的路径数。
这就非常无敌了。
3. OGF 的封闭形式
运用生成函数的过程中,为了方便化简,我们常常会将生成函数转化成另一种,叫封闭形式的东西。
比如说 \(\lang 1,1,1,\dots\rang\) 对应的生成函数是 \(F(x)=\sum_{n=0}x^n=1+x+x^2+\cdots\)。你会发现
直接解得
那问题来了,这怎么可能呢?你会发现这个东西只有在 \(x\in(-1,1)\) 时成立啊。
这时候就要注意了,我们这玩意可是形式幂级数,\(x\) 是一个形式符号,无任何意义,所以是可以这么干的!
因此我们来几个常见的生成函数封闭形式。
- \(F(x)=1+x^a+x^{2a}+x^{3a}+\cdots\)
我们考虑直接仿照上面的方法,错位相减有
解得
下面一个式子倒着推,即自然又好记。
- \(F(x)=\dfrac 1 {(1-x)^k}\)
你会发现,这玩意展开以后理应来说是 \(F(x)=(1+x+x^2+\cdots)^k\),考虑这玩意怎么拆。
考虑它的组合意义,\(x^n\) 对应的系数,就应该是走 \(k\) 步,每步可走 \([0,+\infty)\) 格,到达第 \(n\) 格的方案数。发现这不就隔板法吗,\(x^n\) 对应系数就应该是 \(\dbinom{n+k-1}{k-1}\)。
最后展开式是
- \(F(x)=\dbinom m 0+\dbinom m 1 x+\dbinom m2x^2+\cdots\)
这个形式不熟吗,二项式定理啊。
会发现这个东西与上一个式子的封闭形式互为倒数,我们称这个形式幂级数是上一个的逆。
4. OGF 推导通项公式
咕着,把后面速通完了再来。
5. EGF 的定义和用处
指数生成函数(exponential generating function,EGF)定义为形式幂级数:
你发现这玩意的定义跟 OGF 的区别就在于每一项都除了个 \(n!\),很诡异,有什么用呢?
有红黄两种颜色的球,红球取 \(i\) 颗的方案数是 \(a_i\),黄球是 \(b_i\) 颗,求:取 \(k\) 个球排成一排的方案数。
这个题,和上面 OGF 的例题有什么区别呢?注意到多了一个排成一排,意味着我们要考虑拿出来以后的顺序了。
我们依旧像上一个例题,用 \(x^n\) 形象地表示有 \(n\) 个球,设 \(G_1(x)=\sum_{i=0}a_ix^i,G_2(x)=\sum_{i=0}b_ix^i\),分别对应红球的常生成函数,黄球的常生成函数。
则最终的答案序列是:
其中 \(\dbinom k i\) 表示 \(i\) 个红球 \(k-i\) 个黄球排在一起的方案数,用的插板法思想。这里我们直接组合数拆开。
所以说
也就是说,最后答案对应的 OGF \(F(x)\),对应的 EGF \(\hat{F}(x)\),就等于 \(\hat{G_1}(x)\hat{G_2}(x)\)!
6. EGF 的封闭形式
- \(\lang1,1,1,\dots\rang\)
其 EGF 为 \(\hat{F}(x)=e^x=\exp(x)\),涉及到泰勒展开,我不会。
- \(\lang1,-1,1,-1,\dots\rang\)
其 EGF 为 \(\hat{F}(x)=\exp(-x)\),换元带进去即可证明。
- \(\lang1,0,1,0,\dots\rang\)
其 EGF 为 \(\hat F(x)\) 为 \(\dfrac{\exp(x)+\exp(-x)}{2}\),前两式相加消元即可。
文化课做到一万次这个式子,原来这玩意真有用啊。
- \(\lang1,a,a^{\underline2},a^{\underline3},\dots\rang\)
其 EGF 为 \(\hat F(x)=(1+x)^a\),蛤?这个是何意味。
一方面你可以直接求,另一方面,思考组合意义。
我们知道,\(\lang\dbinom a 0,\dbinom a 1,\dbinom a 2,\dots\rang\) 对应的常生成函数也是 \((1+x)^a\)。而 \(a^{\underline{k}}\) 的含义代表在 \(a\) 个元素里有序的选 \(k\) 个元素出来,那么除以一个 \(k!\),不就是无序的在 \(a\) 元素里选 \(k\) 个元素,即 \(\dbinom a k\) 了吗,因此两者是通的。
例题
P6078 Sweets
有 \(n\) 种糖果,每种糖果有 \(m_i\) 个。
选取一些糖果,求糖果数在 \([a,b]\cap N^*\) 的总方案数。
\(1\le n\le 10,0\le a\le b\le 10^7,0\le m_i\le 10^6\)
容易想到把每种糖果的生成函数列出来,第 \(i\) 个的封闭形式为 \(\dfrac{1-x^{m_i+1}}{1-x}\)。
封闭形式全部相乘!就有
前者我们可以直接拆,最多有 \(2^{10}\) 项,设为 \(G(x)\)。
后者,你发现就是上面写过的封闭形式,展开为 \(\displaystyle{\sum_{i=0}\binom{i+n-1}{n-1}}x^i\),设为 \(H(x)\)。
则答案为
对于右边的式子,形式化下来就是求 \(\displaystyle{\sum_{i=0}^n\binom {m+i}m}\)。考虑它在杨辉三角中的位置,加一个 \(\dbinom{m}{m+1}=0\),引起一个连锁反应,答案为 \(\dbinom{m+n+1}{m+1}\)。
带入原式得
注意到模数非质数,怎么办?
首先由于 \(n\le 10\),上下直接硬算。有个猎奇方法,考虑将上面的模数改成 \(n!\cdot P\),然后上面算出来的余数一定是 \(n!\) 的倍数,再除以 \(n!\) 肯定没问题,而且也是模 \(P\) 意义下的答案。
时间复杂度 \(O(bn)\),要对 G[i]==0 的情况剪一下枝,不然要 T 飞。
POJ3734 Blocks
有 \(N\) 块砖,现要将其染成红、蓝、绿或黄色,其中红色绿色必须涂偶数个,求方案数,答案模 \(10007\)。
\(1\le N\le10^9\)
写出答案的 EGF。
然后直接依次展开,省去中间步骤,得
快速幂即可,复杂度 \(O(T\log n)\)。
CF891E Lust
给定 \(n\) 个数 \(a_1,a_2,\dots,a_n\),要进行 \(k\) 次操作,每次操作随机选择一个 \(1\) 到 \(n\) 的整数 \(x\),将 \(a_x\) 减一,并将答案增加除 \(a_x\) 外所有数的成绩。
求最终答案的期望,对 \(10^9+7\) 取模。
\(1\le n\le 5000,1\le k\le 10^9\)
先尝试刻画一下这个问题的最终答案,发现除 \(a_x\) 外这个有点烦,能不能用 \(\prod a_i\) 变形表示出来?
能啊,会发现一次操作增加的量为
你会发现这玩意可以完美与下一次操作抵消,设 \(a_i\) 被操作了 \(b_i\) 次,答案为
现在求后面这坨就行了。把期望拆开,有
多项组合数 \(\dbinom{k}{b_1,b_2,\dots,b_n}\) 可拆开为 \(\dfrac{k!}{b_1!b_2!\cdots b_n!}\),原式可继续化为
注意到 \(b\) 的和是相等的,观察结构,我们可以根据这个设计一个 EGF,答案应当是 \([x^k]\hat F(x)\)。对于每一项,其对应的 EGF
为了方便计算我们把它拆称封闭形式,则有
这样就有
前者可以直接展开,后者直接 \(O(n^2)\) 暴力拆,设拆出来为 \(\sum_{i=0}c_ix^i\)。有
上指标不用到 \(k\) 的原因是 \(c_n\) 以后就都是 \(0\) 了。
则
然后就没了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号