基于MATLAB的相场模型实现与关键算法解析

一、相场模型基础框架

相场法通过连续场变量描述相界面演化，核心方程包括相场动力学方程和自由能泛函。以经典Cahn-Hilliard方程为例：

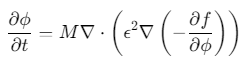
其中：

• \(ϕ∈[0,1]\)：相场变量（0为液相，1为固相）

• \(M\)：迁移率

• \(ϵ\)：界面厚度参数

• \(f(ϕ)\)：自由能密度函数（常用双阱势：\(f(ϕ)=\frac{1}{4}(1−ϕ)^2(1+ϕ)^2\)

---

二、MATLAB核心代码实现

1. 参数初始化

% 网格参数
Lx = 100; Ly = 100; % 计算域尺寸
Nx = 256; Ny = 256; % 网格点数
dx = Lx/Nx; dy = Ly/Ny; % 空间步长
x = linspace(0, Lx, Nx); y = linspace(0, Ly, Ny);
[X, Y] = meshgrid(x, y);

% 物理参数
epsilon = 0.5;    % 界面厚度
M = 0.1;          % 迁移率
tau = 0.01;       % 时间步长
total_time = 100; % 总模拟时间

2. 相场变量初始化

% 初始条件：中心球形晶核
phi = zeros(Ny, Nx);
center = [Ny/2, Nx/2];
r = 10; % 晶核半径
for i = 1:Ny
    for j = 1:Nx
        if norm([i-j, j-i](@ref)-center) < r
            phi(i,j) = 1;
        end
    end
end

3. 相场演化主循环

% 时间推进
for t = 1:total_time
    % 计算化学势
    [dphi_dx, dphi_dy] = gradient(phi, dx, dy);
    d2phi_dx2 = del2(phi, dx);
    d2phi_dy2 = del2(phi, dy);
    curvature = d2phi_dx2 + d2phi_dy2;
    
    % Cahn-Hilliard方程离散
    phi_new = phi + tau*M*(epsilon^2*(dphi_dx.^2 + dphi_dy.^2) - curvature);
    
    % 边界条件（Neumann零通量）
    phi_new(:,1) = phi(:,1);
    phi_new(:,end) = phi(:,end);
    phi_new(1,:) = phi(1,:);
    phi_new(end,:) = phi(end,:);
    
    % 更新相场
    phi = phi_new;
    
    % 可视化（每10步更新）
    if mod(t,10) == 0
        imagesc(phi);
        colormap(gray);
        title(sprintf('Time = %.1f', t*tau));
        drawnow;
    end
end

---

三、关键算法扩展

1. 各向异性界面处理

引入方向依赖的界面能：

% 各向异性函数（四次谐波）
gamma = 1 + 0.1*cos(4*atan2(dphi_dy, dphi_dx));
% 修改迁移率项
M_aniso = M .* gamma;

2. 溶质场耦合（Karma模型）

% 溶质场初始化
c = 0.5*ones(Ny,Nx);

% 溶质扩散方程
for t = 1:total_time
    dc = diffusion(c, D, dx, dy);
    c = c + dt*dc;
end

function dc = diffusion(c, D, dx, dy)
    [dcdx, dcdy] = gradient(c, dx, dy);
    d2cdx2 = del2(c, dx);
    d2cdy2 = del2(c, dy);
    dc = D*(d2cdx2 + d2cdy2);
end

3. 温度场耦合（凝固模拟）

% 温度场初始化
T = 1.0*ones(Ny,Nx);

% 热传导方程
for t = 1:total_time
    dT = heat_conduction(T, k, dx, dy);
    T = T + dt*dT;
end

function dT = heat_conduction(T, k, dx, dy)
    [dTdx, dTdy] = gradient(T, dx, dy);
    d2Tdx2 = del2(T, dx);
    d2Tdy2 = del2(T, dy);
    dT = k*(d2Tdx2 + d2Tdy2);
end

---

四、高级应用案例

1. 枝晶生长模拟

% 各向异性参数
epsilon_aniso = 0.3;
aniso_strength = 0.1;

% 修改化学势计算
curvature_aniso = curvature + aniso_strength*(1 - 2*phi);
phi_new = phi + tau*M*(epsilon_aniso^2*(dphi_dx.^2 + dphi_dy.^2) - curvature_aniso);

2. 三维相场模拟

% 三维网格
Lz = 50; Nz = 128;
[X, Y, Z] = ndgrid(x, y, linspace(0, Lz, Nz));

% 三维Cahn-Hilliard方程
[dx, dy, dz] = ndgrid(dx, dy, dz);
[gradX, gradY, gradZ] = ndgrid(dX, dY, dZ);
lap = del2(X, dx) + del2(Y, dy) + del2(Z, dz);

参考代码 使用MATLAB编写的相场模型 www.youwenfan.com/contentcnq/53396.html

五、可视化与后处理

1. 相场动态演化

% 4D数据可视化（时间-空间-相场）
h = vol3d('CData', phi, 'texture', '3D');
set(h, 'XData', x, 'YData', y, 'ZData', z);
axis equal; view(3); shading interp;

2. 等值面提取

% 提取φ=0.5等值面
fv = isosurface(X, Y, Z, phi, 0.5);
patch(fv, 'FaceColor', 'r', 'EdgeColor', 'none');
isonormals(X, Y, Z, phi, fv);

---

六、典型应用场景

场景	关键参数	验证指标
金属凝固	过冷度ΔT=150K	晶粒尺寸分布
枝晶生长	各向异性强度ε=0.1	二次枝晶臂间距
裂纹扩展	临界能量释放率G_c=1J/m²	裂纹路径偏转角
聚合物共混	界面张力σ=0.5mN/m	相区面积变化率