wqs二分
前置知识
二分,函数的凸/凹性。
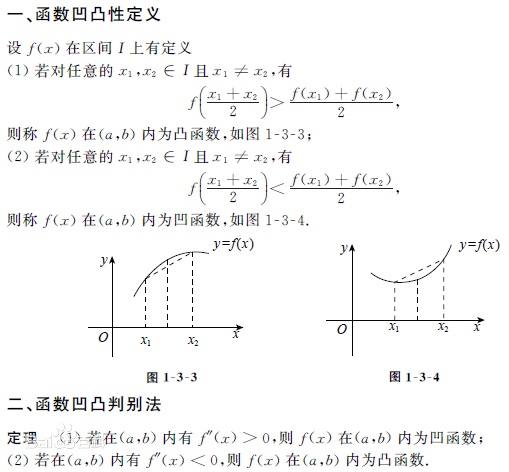
对于凹凸性的定义有不同的说法,但这不是关键。
适用范围:
给定一些带有价值的物品,价值可以为负,对物品的选择有一定的限制(尤其是恰好多少个之类的)
求选定物品总价值的最值。
大致思路:
以 例题 做讲解。
首先我们发现如果没有这个恰好白边的限制,很明显直接做最小生成树就可以了。问题的关键在于白边数量的限制,所以答案一定与白边数量的有关。
所以我们设一个函数为 \(f(x)\) 表示恰好选 \(x\) 条白边的答案,我们要的就是 \(f(k)\) 。然后我们发现,虽然不知道这个具体的形式,但我们知道 \(f(x)\) 一定是凹函数,斜率一定是单调不降的。
如何证明?我们可以感性理解,我们先只有黑边建生成树(我们假设为存在),然后替换白边,显然开始的白边对答案贡献最小,随着白边数量的增加,我们选择的白边会越来越不优。(不然为什么不交换顺序使答案更优)。所以我们可以合理猜测,它的图像长成这样(图片来自Dfkuaid的博客)。

然后你发现这并没有什么用,我们还是不会求 \(f(k)\) 的值。这时候,神明给了我们指引,我们考虑二分斜率。对于这个斜率的直线会切到函数图像上的一个点而我们可以算到这个点,根据这个点的横坐标我们可以知道我们要的 \(k\) 需要增加斜率或减少斜率,通过这样的调整在最后我们就可以恰好切到 \((k,f(k))\) 就得到了答案。
现在问题变成了如何求相切的点?对于每一个点我们做一条给定斜率的直线,我们发现相切的点有一个特殊性质,就是纵截距最小。我们可以如何应用的这个点,根据初中知识我们知道纵截距 \(b=f(x)-kx\) 我们考虑它的实际含义是什么,就是每次选一个限制的边就减 \(k\) ,这样的最小值。实现就是做 MST 之前,将所有白边都减去 \(k\) 。
我们发现通过一些改变,我们就变成了一个没有加限制的MST(唯一不同的是要记录 \(x\) ,二分的过程有用)。代码就比较简单了。
#include <bits/stdc++.h>
using namespace std;
int v,e,ne,fa[50010],sum,cnt,tmp,ans;
struct node
{
int qd,zd,jz,cl;
}a[100010];
bool cmp(node x,node y)
{
if(x.jz!=y.jz )return x.jz<y.jz;
else return x.cl <y.cl;
}
int find(int x)
{
if(fa[x]==x)return x;
else
{
fa[x]=find(fa[x]);
return fa[x];
}
}
void kruskal()
{
sum=0,cnt=0,tmp=0;
for(int i=1;i<=v;i++)fa[i]=i;
for(int i=1;i<=e;i++)
{
int f1=find(a[i].qd);
int f2=find(a[i].zd);
if(f1!=f2)
{
cnt++;
fa[f2]=f1;
sum+=a[i].jz;
if(a[i].cl==0)tmp++;
if(cnt==v-1)return;
}
}
return;
}
int main()
{
scanf("%d%d%d",&v,&e,&ne);
for(int i=1;i<=e;i++)
{
scanf("%d%d%d%d",&a[i].qd,&a[i].zd,&a[i].jz,&a[i].cl);
a[i].qd+=1;a[i].zd+=1;
}
int l=-110,r=110;
while(l<=r)
{
int mid=(l+r)>>1;
for(int i=1;i<=e;i++)
if(a[i].cl==0)a[i].jz+=mid;
sort(a+1,a+e+1,cmp);
kruskal();
if(tmp>=ne)
{
ans=sum-ne*mid;
l=mid+1;
}
else r=mid-1;
for(int i=1;i<=e;i++)
if(a[i].cl==0)a[i].jz-=mid;
}
printf("%d\n",ans);
return 0;
}
更为简单的理解方式
wqs二分还有一个别的名字,带权二分。我们可以理解为对于对限制有影响的权值我们添加一个附加值,在要答案最小的时候,我们发现选的多了,就将附加值调大,这样再做的时候选的就会变少,同理选少了,减少就会多选。
比如例题,我们将白边的权值减少了,我们做最小生成树的时候就可能多选白边。一直调整附加值,直到恰好选了 \(k\) 个边。
注意事项
刚才的推论看似很完美,但是我们注意到有可能出现一种情况,我们证明的斜率单调不降,这意味着可能出现斜率相同的情况。
如果我们要的是有 \(j\) 条白边,但是我们做MST中选边的时候可能在白边和黑边相等的时候选择了白边,就可能选到 \(i\) ,用上面的代码就会出问题。所以我们需要提前钦定在边权相同时优先选白边(排序时处理)。
在更一般的情况下,这个问题就是二分的时候,等号应该取在小于时还是大于时。对于斜率相同的点在转移时应该考虑相等时如何选择对应二分时的选择。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号