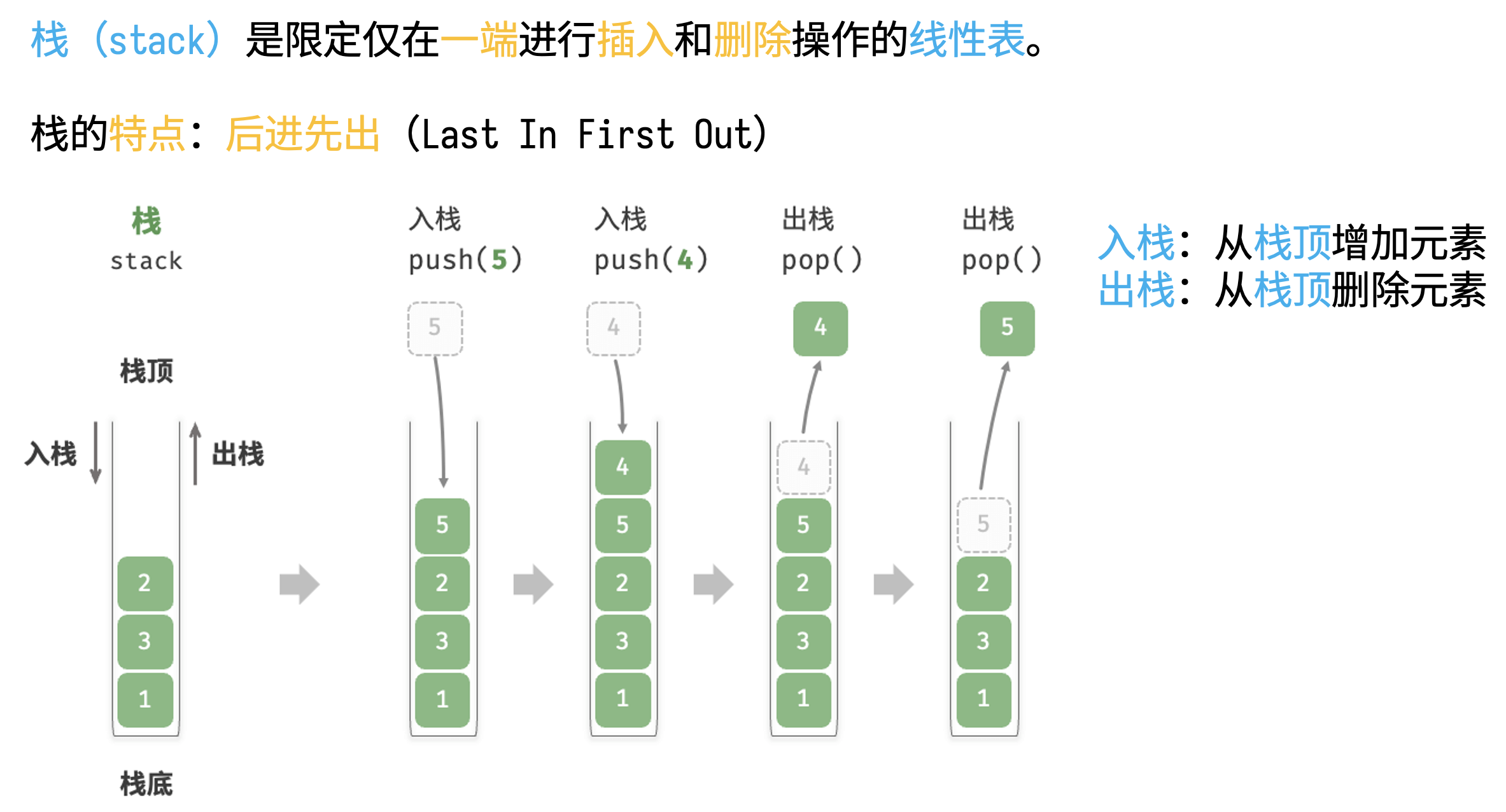
栈

在超市购物的时候，超市入口处往往会放一排购物车。这一排购物车一个插在另一个的后面，顺序排列，第一个一般靠着墙，不好拿。这时候，如果想取走一辆，一般是先取走最后面的一辆，下一个来购物的顾客取走倒数第二辆。与之对应的，如果顾客用完了购物车，要把购物车还回去，那么归还的这辆购物车通常也是放在最后面。在通常情况下，最后面的车会被反复取用，而第一辆很少被用到，除非其他购物车都被取走了。

---

选择题：今有一空栈 S，对下列待进栈的数据元素序列 a,b,c,d,e,f 依次进行：进栈，进栈，出栈，进栈，进栈，出栈的操作，则此操作完成后，栈底元素为？

• A. b
• B. a
• C. d
• D. c

答案

B。

[] → [a] → [a,b] → [a] → [a,c] → [a,c,d] → [a,c]

所有操作完成后，栈中还剩下两个元素，从栈底到栈顶依次是 a 和 c。

---

例题：UVA673 平衡的括号 Parentheses Balance

将这个字符串从左往右写，一旦遇到匹配上的括号，就把这对括号擦掉，就像“消消乐”一样。

以 [([])()] 为例，从左往右写，写到 [([]，产生了匹配。所以把 [] 擦掉，字符串变成了 [(。接下来一个字符是 )，字符串变成了 [()，产生了匹配。擦掉 ()，纸上只剩下了一个 [。接下来加一个字符变成 [(，没有产生匹配。再加一个，变成 [()，擦掉 ()，只剩下一个 [。接下来加上 ]，产生了匹配，擦掉 [] 之后字符串变为空。因此，所给的字符串是合法的。

如果依次处理完字符串的所有字符，发现还剩下有括号，那么就说明有些括号没有被匹配到，说明是非法的括号序列。比如 ([)(]) 根据上面的做法，就可以知道这是一个非法的序列。

参考代码

#include <iostream>
#include <string>
#include <stack>
using namespace std;

// 辅助函数：判断两个括号是否配对
bool is_pair(char open, char close) {
    if (open == '(' && close == ')') return true;
    if (open == '[' && close == ']') return true;
    return false;
}

int main()
{
    int n;
    // 读取测试用例的数量
    cin >> n;
    
    string line;
    // 消耗掉读取 n 后残留在缓冲区中的换行符，确保 getline 能正确读取后续行
    getline(cin, line);

    while (n--) {
        // 读取整行输入，因为题目规定空串也是合法的，所以必须用 getline
        getline(cin, line);
        
        stack<char> st;
        bool ok = true;
        
        // 遍历字符串中的每一个字符
        for (char c : line) {
            // 如果是左括号，直接压入栈中
            if (c == '(' || c == '[') {
                st.push(c);
            } 
            // 如果是右括号
            else {
                // 检查栈是否不为空，且栈顶括号与当前右括号是否匹配
                if (!st.empty() && is_pair(st.top(), c)) {
                    st.pop(); // 匹配成功，弹出栈顶
                } else {
                    // 栈为空（没有对应的左括号）或不匹配，标记为不合法并跳出
                    ok = false; 
                    break;
                }
            }
        }
        
        // 最终判断：如果中途没有出错且栈恰好为空（所有左括号都已匹配），则输出 Yes
        if (ok && st.empty()) cout << "Yes\n";
        else cout << "No\n";
    }
    return 0;
}

习题：P10472 括号画家

解题思路

最直观的方法是枚举所有可能的子串，并检查它们是否是美观的。先枚举起点 \(i\)，再枚举终点 \(j \ (j \ge i)\)，检查子串 \(i \sim j\) 是否合法。检查一个括号序列是否合法可以使用栈：遇到左括号入栈；遇到右括号，看栈顶括号是否匹配，匹配则弹出，否则非法；扫描结束后栈为空则合法。枚举起点、终点的时间复杂度是 \(O(N^2)\)，一次括号匹配问题检查的时间复杂度是 \(O(N)\)，总时间复杂度达到 \(O(N^3)\)，会超时。

实际上当起点固定时，对于不同的终点实际上是共享同一段前缀的，因此枚举终点和检查子串这两步可以放在一起进行，这样时间复杂度降到 \(O(N^2)\)。

参考代码

#include <cstdio>
#include <cstring>
#include <stack>
#include <algorithm>
using namespace std;

const int N = 1e4 + 5;
char s[N];

// 辅助函数：判断两个括号字符是否配对
bool is_pair(char open, char close) {
    if (open == '(' && close == ')') return true;
    if (open == '[' && close == ']') return true;
    if (open == '{' && close == '}') return true;
    return false;
}

int main()
{
    // 读取输入的括号序列
    scanf("%s", s);
    int n = strlen(s);
    int ans = 0;

    // 枚举每一个可能的子串起始位置 i
    for (int i = 0; i < n; i++) {
        // 美观（合法）的括号序列必然以左括号开头
        if (s[i] != '(' && s[i] != '[' && s[i] != '{') continue;
        
        // 使用栈来检查从 i 开始的子串是否匹配
        stack<char> st;
        for (int j = i; j < n; j++) {
            // 如果是左括号，入栈其下标
            if (s[j] == '(' || s[j] == '[' || s[j] == '{') {
                st.push(s[j]);
            } 
            // 如果是右括号，检查是否与栈顶匹配
            else if (!st.empty() && is_pair(st.top(), s[j])) {
                st.pop(); // 匹配成功，弹出栈顶
            } 
            else {
                // 如果遇到无法匹配的右括号，或者栈为空时的右括号，说明从 i 开始的这段序列已断裂
                break;
            }
            
            // 如果此时栈为空，说明子串 s[i...j] 是一个完整的、美观的括号序列
            if (st.empty()) {
                ans = max(ans, j - i + 1);
            }
        }
    }

    // 输出最长长度
    printf("%d\n", ans);
    return 0;
}

例题：P4387 【深基15.习9】验证栈序列

给定两个序列，保证序列一定是 \(1\) 到 \(n\) 的某个排列，判断按照第一个序列中的顺序入栈是否有可能产生出栈序列去匹配第二个序列。

解决这个问题的最直接方法就是模拟整个过程，可以借助一个辅助栈，严格按照入栈序列的顺序将元素压入，并在适当的时候检查是否能匹配出栈序列。

具体步骤如下：

1. 创建一个空的辅助栈 \(s\)。
2. 使用两个索引，一个 \(p\) 指向入栈序列 \(in\) 的当前元素，一个 \(i\) 指向出栈序列 \(out\) 的当前元素。
3. 遍历出栈序列 \(out\) 中的每一个元素 \(out_i\)，对于当前的 \(out_i\)，考虑它能被合法地弹出吗？
4. 一个元素能被弹出的唯一前提是它正位于栈顶。
5. 因此，检查辅助栈 \(s\) 的栈顶。
   • 如果栈为空，或者栈顶元素不是期望弹出的 \(out_i\)，就必须从入栈序列 \(in\) 中继续压入元素，直到栈顶是想要的 \(out_i\) 为止，不断地执行入栈动作并递增 \(p\)。
   • 如果在所有 \(in\) 序列的元素都压入栈后，栈顶依然不是 \(out_i\)，那就意味着 \(out_i\) 永远无法在这个时间点被弹出。因此，这个出栈序列是不合法的。
   • 如果经过若干次（可能 0 次）压栈后，栈顶元素成功变成了 \(out_i\)，那就说明这个弹出操作是合法的。立即将该元素从辅助栈 \(s\) 中弹出，并继续考察出栈序列的下一个元素 \(out_{i+1}\)。
6. 如果能顺利地遍历完整个出栈序列 \(out\)，并成功匹配和弹出了所有 \(n\) 个元素，那么这个序列就是合法的。反之，如果在任何一步卡住了，它就是不合法的。

参考代码

#include <cstdio>
#include <stack> // 引入栈容器

using namespace std;

const int N = 100005; // 定义数组最大长度
int in[N];  // 存储入栈序列
int out[N]; // 存储出栈序列

// 处理单次查询的函数
void solve() {
    int n; 
    scanf("%d", &n); // 读取序列长度

    // 读取 n 个数作为入栈序列
    for (int i = 1; i <= n; i++) {
        scanf("%d", &in[i]);
    }
    // 读取 n 个数作为出栈序列
    for (int i = 1; i <= n; i++) {
        scanf("%d", &out[i]);
    }

    stack<int> s; // 辅助栈，用于模拟实际的栈操作
    int p = 1;      // 指向下一个要入栈的元素在 in 序列中的位置

    // 遍历给定的出栈序列 out
    for (int i = 1; i <= n; i++) {
        // 当栈为空，或者栈顶元素不等于当前期望出栈的元素时，
        // 就需要从入栈序列 in 中继续获取元素并压入栈中。
        // 同时要保证 p 没有越界。
        while (p <= n && (s.empty() || s.top() != out[i])) {
            s.push(in[p]); // 将 in[p] 压入辅助栈
            p++;           // p 指向下一个
        }

        // 经过上面的 while 循环后，检查栈顶元素是否是期望出栈的元素
        // 如果是，说明本次出栈操作合法
        if (!s.empty() && s.top() == out[i]) {
            s.pop(); // 模拟出栈
        } 
        // 如果不是，说明已经无法让 out[i] 合法出栈，提前结束
        else {
            printf("No\n");
            return;
        }
        
    }

    // 如果前面没有判断出 No，说明这个出栈序列能匹配成功
    printf("Yes\n");
}

int main()
{
    int q; 
    scanf("%d", &q); // 读取询问次数
    // 循环处理 q 次询问
    for (int i = 1; i <= q; i++) {
        solve();
    }
    return 0;
}

---

选择题：若元素 a、b、c、d、e、f 依次进栈，允许进栈、退栈操作交替进行，但不允许连续三次退栈操作，则不可能得到的出栈序列是？

• A. dcebfa
• B. cbdaef
• C. bcaefd
• D. afedcb

答案

正确答案是 D。

1. a 进栈，栈：[a]
2. a 出栈（第 1 次连续出栈），序列：a，栈：[]
3. 为了让 f 出栈，必须将 b, c, d, e, f 全部依次进栈，栈：[b, c, d, e, f]
4. f 出栈（第 1 次连续出栈），序列：af，栈：[b, c, d, e]
5. e 出栈（第 2 次连续出栈），序列：afe，栈：[b, c, d]
6. d 出栈（第 3 次连续出栈），序列：afed，栈：[b, c]，此时发生了连续三次出栈（f, e, d），违反了“不允许连续三次退栈操作”的规则。

因此，序列 afedcb 是不可能得到的。

例题：P2201 数列编辑器

需要维护一个整数数列和一个光标，支持以下 5 种操作：

1. I x：在光标前插入数字 \(x\)。
2. D：删除光标前的一个数字。
3. L：光标左移（相当于光标越过左边的一个数字）。
4. R：光标右移（相当于光标越过右边的一个数字）。
5. Q k：询问光标左侧数列中，前 \(k\) 个数构成的所有前缀和中的最大值。

总共有 \(N\) 个操作，数据范围 \(N \le 10^6\)。

本题的特殊之处在于，I,D,L,R 四种操作都在光标位置处发生，并且操作完成后光标至多移动 1 个位置。根据这种“始终在序列中间某个指定位置进行修改”的性质，可以考虑对顶栈。左栈存储光标左侧的所有数字，栈顶元素紧邻光标左侧。右栈存储光标右侧的所有数字，栈顶元素紧邻光标右侧。

通过这两个栈，各种操作可以映射如下：

• I x：将 \(x\) 压入左栈。
• D：左栈弹出一个元素。
• L：左栈弹出一个元素，压入右栈。
• R：右栈弹出一个元素，压入左栈。

这样，所有修改和移动操作的时间复杂度均为 \(O(1)\)。

题目要求查询 Q k，即光标左侧数列 \(a_1, \dots, a_n\) 中，前 \(k\) 个数字对应的最大前缀和 \(\max\limits_{1 \le i \le k} (\sum\limits_{j=1}^i a_j)\)。由于查询总是针对光标左侧的数列，也就是针对左栈中的元素，可以在左栈入栈时同步维护相关信息。（定义辅助数组 \(s_i\) 维护左栈中从栈底到第 \(i\) 个元素的前缀和，\(f_i\) 维护左栈中前 \(i\) 个元素的所有前缀和中的最大值）

参考代码

#include <cstdio>
#include <algorithm>
using namespace std;

const int N = 1e6 + 5;
const int INF = 1e9;

// l[N], r[N]: 对顶栈结构。
// l 栈存储光标左侧的数列，p 为栈顶指针。
// r 栈存储光标右侧的数列，q 为栈顶指针。
// sum[i]: 光标左侧前 i 个数的前缀和。
// f[i]: 光标左侧前 i 个数的前缀和中的最大值，即 max(sum[1], ..., sum[i])。
int f[N], l[N], r[N], sum[N];
char op[2];

int main()
{
    int n; scanf("%d", &n);
    
    f[0] = -INF;
    int p = 0, q = 0; // p 指向光标左侧栈顶，q 指向光标右侧栈顶
    
    while (n--) {
        scanf("%s", op);
        if (op[0] == 'I') {
            // I x: 在光标前插入 x
            int x; scanf("%d", &x);
            l[++p] = x;                 // 入左栈
            sum[p] = sum[p - 1] + x;    // 更新前缀和
            f[p] = max(f[p - 1], sum[p]); // 更新最大前缀和
        } else if (op[0] == 'D') {
            // D: 删除光标前的数字
            if (p > 0) p--; // 左栈弹栈，前缀信息自然失效，无需额外清除
        } else if (op[0] == 'L') {
            // L: 光标左移
            // 相当于把光标左侧的一个数移到光标右侧
            if (p > 0) {
                r[++q] = l[p--]; // 左栈出，右栈入
            }
        } else if (op[0] == 'R') {
            // R: 光标右移
            // 相当于把光标右侧的一个数移到光标左侧
            if (q > 0) {
                int val = r[q--]; // 右栈出
                l[++p] = val;     // 左栈入
                // 因为进入了左栈，需要重新维护前缀信息
                sum[p] = sum[p - 1] + val;
                f[p] = max(f[p - 1], sum[p]);
            }
        } else {
            // Q k: 询问第 k 位及之前的最大前缀和
            int k; scanf("%d", &k);
            printf("%d\n", f[k]);
        }
    }
    return 0;
}