D. Fibonacci Paths

D. Fibonacci Paths

You are given a directed graph consisting of $n$ vertices and $m$ edges. Each vertex $v$ corresponds to a positive number $a_v$. Count the number of distinct simple paths$^{\text{∗}}$ consisting of at least two vertices, such that the sequence of numbers written at the vertices along the path forms a generalized Fibonacci sequence.

In this problem, we will consider that the sequence of numbers $x_0, x_1, \ldots, x_k$ forms a generalized Fibonacci sequence if:

• $x_0, x_1$ are arbitrary natural numbers.
• $x_i = x_{i - 2} + x_{i - 1}$ for all $2 \le i \le k$.

Note that a generalized Fibonacci sequence consists of at least two numbers.

Since the answer may be large, output it modulo $998\,244\,353$.

$^{\text{∗}}$A simple path in a directed graph is a sequence of vertices $v_1, v_2, \ldots, v_k$ such that each vertex in the graph appears in the path at most once and there is a directed edge from $v_i$ to $v_{i+1}$ for all $i < k$.

Input

Each test contains multiple test cases. The first line contains the number of test cases $t$ ($1 \le t \le 10^4$). The description of the test cases follows.

The first line of each test case contains two numbers $n$, $m$ ($2 \le n \le 2 \cdot 10^5$, $1 \le m \le 2 \cdot 10^5$) — the number of vertices and the number of edges in the graph, respectively.

The second line of each test case contains $n$ natural numbers $a_1, a_2, \ldots, a_n$ ($1 \le a_i \le 10^{18}$) — the numbers written at the vertices.

The next $m$ lines contain the edges of the graph; each edge is defined by two natural numbers $v, u$ ($1 \le v, u \le n$, $u \neq v$), denoting a directed edge from $v$ to $u$. It is guaranteed that there are no multiple edges in the graph.

It is guaranteed that the sum of $n$ and the sum of $m$ across all test cases do not exceed $2 \cdot 10^5$.

Output

For each test case, output the number of paths that form a generalized Fibonacci sequence, modulo $998\,244\,353$.

Example

Input

4
4 4
3 4 3 6
1 2
1 3
2 4
3 4
4 6
1 1 1 2
1 2
2 3
3 1
1 4
2 4
3 4
8 11
2 4 2 6 8 10 18 26
1 2
2 3
3 1
4 3
2 4
3 5
5 6
4 6
6 7
7 5
5 8
2 2
10 10
1 2
2 1

Output

5
9
24
2

Note

Explanation of the first test case example (the vertex number is outside the brackets, the number written in the vertex is inside):

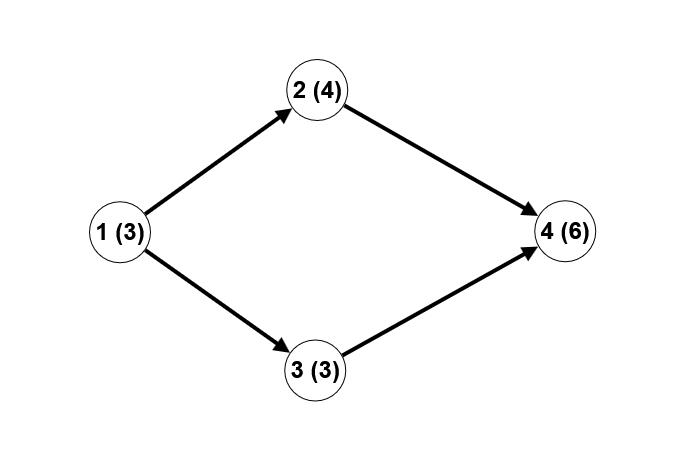
In this case, there are 5 generalized Fibonacci paths: ($1, 2$), ($1, 3$), ($2, 4$), ($3, 4$), ($1,3,4$). For example, for the path ($1,3,4$), the sequence of numbers written at the vertices along this path is: [$3,3,6$]. As can be easily seen, the third number in the sequence is the sum of the two previous ones.
Explanation of the second test case example:

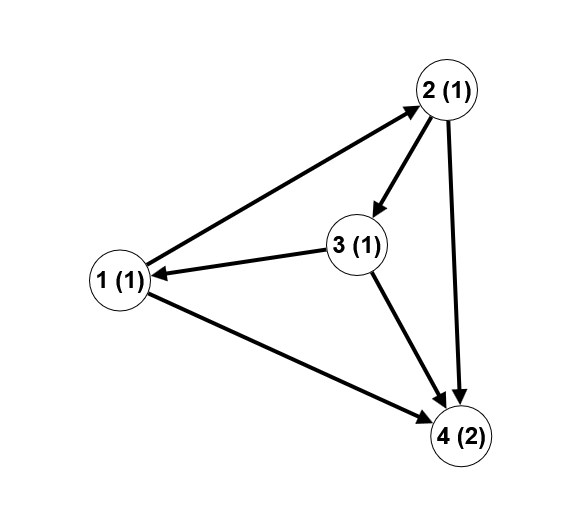
In this case, there are 9 generalized Fibonacci paths: ($1, 2$), ($1, 4$), ($2, 3$), ($2, 4$), ($3, 1$), ($3, 4$), ($1, 2, 4$), ($2, 3, 4$), ($3, 1, 4$). Note that for the path ($1, 2, 3$), the sequence of numbers written at the vertices along this path is: [$1,1,1$], and it is not a generalized Fibonacci sequence.

 

解题思路

  因为构成路径的节点权值需要满足广义斐波那契数列的要求，路径的最大长度会受到限制（通过打表可以得知路径长度不会超过 $87$）。然而本题并没有用到该性质。

  考虑路径中的一条边 $(u, v)$，下一条边应该满足 $(v, w) \in E$ 且 $a_w = a_u + a_v$。可以发现，路径中相邻两条边的端点权值之和是递增的，即对于路径中的相邻两条边 $(u, v)$ 和 $(v, w)$，必定有 $a_u + a_v < a_v + a_w$。这意味着在选择路径的下一条边时，路径不会形成环。基于这一观察，我们可以用 dp 来求解问题，定义状态 $f(u, v)$ 表示以边 $(u, v)$ 为路径的首条边时，能够构造出的满足广义斐波那契数列的不同路径数量。状态转移方程为 $$f(u, v) = 1 + \sum_{\begin{array}{c} (v, w) \in E \\ a_w = a_u + a_v \end{array}} f(v, w)$$

  需要注意的是，dp 的计算顺序应当按照边的两个端点的权值和递降的顺序进行计算，因为路径中下一条边的两个端点权值一定大于上一条边的两个端点权值。这样，我们能够确保在计算 $f(u, v)$ 时，所有满足条件的 $f(v, w)$ 都已被计算过。

  由于转移时需要枚举每个 $u$ 的所有出边，最坏情况下时间复杂度是 $O(m^2)$，可以参考下面的图：

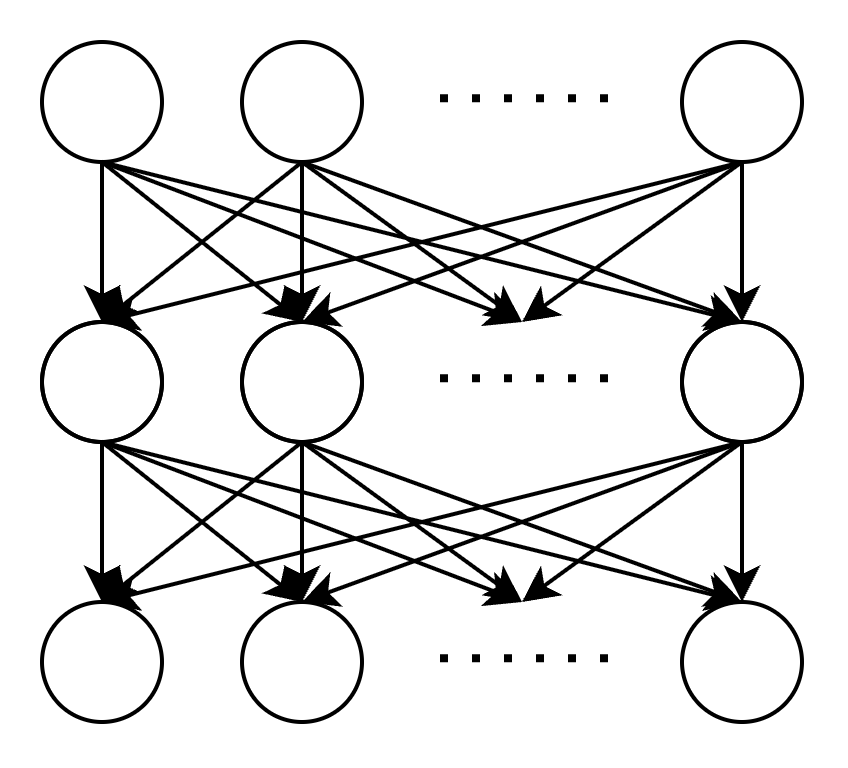
  在计算 $f(u,v)$ 时，是否真的有必要枚举 $v$ 的所有出边？有没有更快的方法找到既是 $v$ 的出边又满足 $a_w = a_u + a_v$ 的边？为此，我们可以记录每条边 $(u,v)$，源点 $u$ 和目标节点 $v$ 权值 $a_v$ 的对应状态 $f(u,v)$，记为 $g(u, a_v)$。这样，$f(u,v)$ 的转移方程就可以简化为 $f(u,v) = g(v, a_u + a_v) + 1$，同时更新 $g(u,a_v) \gets g(u,a_v) + f(u,v)$。我们可以将其合并，只需重新定义状态 $f(u, a_v)$，表示以源点 $u$ 目标节点 $v$ 的权值 $a_v$ 对应的边 $(u,v)$ 为路径的首条边时，能够构造出的满足广义斐波那契数列的不同路径数量。此时，状态转移方程为 $f(u,a_v) = f(v, a_u + a_w) + 1$。

  最终的答案即为所有以边为起点的广义斐波那契路径的总和 $\sum\limits_{(u,v) \in E}{f(u,a_v)}$。

  AC 代码如下，时间复杂度为 $O(m\log{m})$：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const int N = 2e5 + 5, mod = 998244353;

LL a[N];
array<int, 2> p[N];
map<LL, int> f[N];

void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 0; i < m; i++) {
        cin >> p[i][0] >> p[i][1];
    }
    sort(p, p + m, [&](auto &p, auto &q) {
        return a[p[0]] + a[p[1]] > a[q[0]] + a[q[1]];
    });
    for (int i = 1; i <= n; i++) {
        f[i].clear();
    }
    for (int i = 0; i < m; i++) {
        int u = p[i][0], v = p[i][1];
        f[u][a[v]] = (f[u][a[v]] + f[v][a[u] + a[v]] + 1) % mod;
    }
    int ret = 0;
    for (int i = 1; i <= n; i++) {
        for (auto &[x, y] : f[i]) {
            ret = (ret + y) % mod;
        }
    }
    cout << ret << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    
    return 0;
}

 

解题思路

  Codeforces Round 1070 (Div.2) Editorial：https://codeforces.com/blog/entry/149154