FWT
这是肥王豚!!!
FWT
大部分是抄oiwiki的……
oiwiki说:在算法竞赛中,FWT 是用于解决对下标进行位运算卷积问题的方法。
公式:\(C_i=\sum_{i=j\oplus k}A_jB_k\)。
FWT 和 FFT 很像,都是对序列进行变换,然后对位相乘再逆变换回去。
我们记 \(A\) 序列变换后是 \(FWT[A]\),\(n\) 为所有序列的长度并且保证 \(n=2^k,k\in \mathbb{N}\)。
设 \(c(i,j)\) 为 \(A_j\) 对 \(FWT[A]_i\) 的贡献系数,因为 \(FWT[A]_iFWT[B]_i=FWT[C]_i\),拆开来可得 \(\sum_{j=0}^{n-1} c(i,j)C_j=\sum_{j=0}^{n-1}\sum_{k=0}^{n-1}c(i,j)c(i,k)A_jB_k\),再把 \(C_j\) 拆成上面的柿子,要满足柿子成立需要满足 \(c(i,j\oplus k)=c(i,j)c(i,k)\)。
同时贡献函数 \(c\) 还需要满足可以按位处理,既 \(c(i,j)=\prod_{o\ge 0,2^o<n}c_o(i 的第 o 位,j 的第 o 位)\),才可以用 FWT(默认下面每一位的 \(c_o\) 相同)。如果可以按位处理,我们就可以递归:\(FWT[A]_i=\sum_{j=0}^{n-1}c(i,j)A_j=\sum_{j=0}^{n/2-1}c(i,j)A_j+\sum_{j=n/2}^{n-1}c(i,j)A_j\),相当于是按最高位分类,因为可以按位处理,设 \(i\) 的最高位为 \(x\),去掉最高位的数为 \(o'\),则柿子 \(=c(x,0)\sum_{j=0}^{n/2-1}c(i',j')A_j+c(x,1)\sum_{j=n/2}^{n-1}c(i',j')A_j=c(x,0)FWT[A_0]_{i'}+c(x,1)FWT[A_1]_{i'}\),其中 \(A_0\) 是前半段,\(A_1\) 是后半段。
可以发现这么递归,只会用到 \(c(0,0),c(0,1),c(1,0),c(1,1)\),写成矩阵形式 \(\begin{bmatrix} c(0,0)&c(0,1)\\ c(1,0)&c(1,1) \end{bmatrix}\)
逆变换时,流程还是一样,我们只需要对上面矩阵求逆就好了(不需要满足 \(c(i,j\oplus k)=c(i,j)c(i,k)\) 了)。为什么是从上往下递归而不是从下往上递归?感性理解就是每一位是分开处理,对某一位做一遍相当于让这一位贡献失效。当然可能只有我有这个问题?
或运算
就是把一开始的公式的 \(\oplus\) 设为 \(\cup\),后不赘述。
构造 \(FWT[A]_i=\sum_{i=i\cup j}A_j\),此时 \(c=\begin{bmatrix} 1&0\\ 1&1 \end{bmatrix}\),满足条件,逆变换矩阵为 \(\begin{bmatrix} 1&0\\ -1&1 \end{bmatrix}\)。
与运算
构造 \(FWT[A]_i=\sum_{i=i\cap j}A_j\),此时 \(c=\begin{bmatrix} 1&1\\ 0&1 \end{bmatrix}\),满足条件,逆变换矩阵为 \(\begin{bmatrix} 1&-1\\ 0&1 \end{bmatrix}\)。
异或运算
设 \(x\circ y=popcnt(x\cap y) \bmod 2\)。
构造 \(FWT[A]_i=\sum_{i\circ j=0}A_j-\sum_{i\circ j=1}A_j\),此时 \(c=\begin{bmatrix} 1&1\\ 1&-1 \end{bmatrix}\),满足条件,逆变换矩阵为 \(\begin{bmatrix} 0.5&0.5\\ 0.5&-0.5 \end{bmatrix}\)。
FWT 是线性变换
FWT 是线性变换,满足 \(FWT[A+B]=FWT[A]+FWT[B],FWT[c\cdot A]=c\cdot FWT[A]\)。
好吧我也不了解线性变换之类的知识,所以后面某些题目某些地方并不能做出解释。
K 维 FWT
一样的套路但是什么是 分原神启动项式,我都不知道从哪学习这玩意,算了当他不考。
题目:
值得一提的是很多高维前缀和的题目都被打上了 FWT 标签,然后在理论难度的时候就有人说 FWT 都是紫的了这题也得紫,难蚌……
P4717 【模板】快速莫比乌斯 / 沃尔什变换 (FMT / FWT)
按上面做就好了
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=18,S=1<<N,mod=998244353;
int n,a[S],b[S],A[S],B[S];
void Or(int *a,int tp){
for(int k=2;k<=1<<n;k<<=1){
int x=k>>1;
for(int i=0;i<1<<n;i+=k)
for(int j=0;j<x;j++)
a[i+j+x]=(a[i+j+x]+a[i+j]*tp)%mod;
}
}
void And(int *a,int tp){
for(int k=2;k<=1<<n;k<<=1){
int x=k>>1;
for(int i=0;i<1<<n;i+=k)
for(int j=0;j<x;j++)
a[i+j]=(a[i+j]+a[i+j+x]*tp)%mod;
}
}
void Xor(int *a,int tp){
for(int k=2;k<=1<<n;k<<=1){
int x=k>>1;
for(int i=0;i<1<<n;i+=k)
for(int j=0;j<x;j++){
int xx=a[i+j+x];
a[i+j+x]=(a[i+j]-xx)%mod*tp%mod;
a[i+j]=(a[i+j]+xx)%mod*tp%mod;
}
}
}
signed main(){
scanf("%lld",&n);
for(int i=0;i<1<<n;i++)scanf("%lld",&a[i]);
for(int i=0;i<1<<n;i++)scanf("%lld",&b[i]);
for(int i=0;i<1<<n;i++)A[i]=a[i],B[i]=b[i];
Or(A,1),Or(B,1);
for(int i=0;i<1<<n;i++)A[i]=A[i]*B[i]%mod;
Or(A,-1);
for(int i=0;i<1<<n;i++)printf("%lld ",(A[i]+mod)%mod);
printf("\n");
for(int i=0;i<1<<n;i++)A[i]=a[i],B[i]=b[i];
And(A,1),And(B,1);
for(int i=0;i<1<<n;i++)A[i]=A[i]*B[i]%mod;
And(A,-1);
for(int i=0;i<1<<n;i++)printf("%lld ",(A[i]+mod)%mod);
printf("\n");
for(int i=0;i<1<<n;i++)A[i]=a[i],B[i]=b[i];
Xor(A,1),Xor(B,1);
for(int i=0;i<1<<n;i++)A[i]=A[i]*B[i]%mod;
Xor(A,mod+1>>1);
for(int i=0;i<1<<n;i++)printf("%lld ",(A[i]+mod)%mod);
printf("\n");
return 0;
}
在 or 卷积的基础上还多了个不能有交集。考虑把 \(a\) 序列每个元素按二进制下 \(1\) 的个数分类。然后每一个类别都做一次 FWT,\(b\) 序列同理,那么 \(FWT[c]_{i,j}=\sum_{x=0}^{i}FWT[a]_{x,j}FWT[b]_{i-x,j}\),最后合法的位置满足 \(i=popcnt(j)\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20,S=1<<N,mod=1e9+9;
int n,o[S],a[N+1][S],b[N+1][S],c[N+1][S];
void FWT(int *a,bool fl){
for(int len=2;len<=1<<n;len<<=1){
int slen=len>>1;
for(int l=0;l<1<<n;l+=len)
for(int k=l;k<l+slen;k++)
a[k+slen]=(a[k+slen]+(fl?a[k]:-a[k]))%mod;
}
}
signed main(){
scanf("%lld",&n);
for(int i=0;i<1<<n;i++){
int x;scanf("%lld",&x);
a[o[i]=__builtin_popcount(i)][i]=x;
}
for(int i=0;i<1<<n;i++){
int x;scanf("%lld",&x);
b[o[i]][i]=x;
}
for(int i=0;i<=n;i++){
FWT(a[i],1),FWT(b[i],1);
for(int j=0;j<1<<n;j++)
for(int k=0;k<=i;k++)
c[i][j]=(c[i][j]+a[k][j]*b[i-k][j])%mod;
FWT(c[i],0);
}
for(int i=0;i<1<<n;i++)
printf("%lld ",(c[o[i]][i]+mod)%mod);
return 0;
}
摘抄 EternalAlexander 的题解。
根据佬的证明得出 \(SG(2^k+n)=n+1(n\in[0,2^k))\)。
所以我们设 \(A_i=\sum_{i=1}^m[SG(i)==i],B=A^{|V|}\)(这里的乘法是异或卷积运算)则选取 \(|V|\) 个数使得异或和为 \(x\) 的方案数即为 \(B_x\)(根据异或卷积的柿子可得)。由于可以点乘,所以 FWT 后每一位都做快速幂就好了。
没写代码。
吓哭了 K-FWT,不会,到时候也许会做的。
最优化不好做,转化为计算每一种答案的生成树个数。题解说矩阵树定理是计算 \(\sum_T \prod_{e\in T}w_e\),只要 \(<W,+,\times>\) 是个环就可以求出这个柿子(真的吗)。所以我们定义 \(\times\) 为题解给的集合卷积,\(+\) 为对位相加。因为 FWT 是线性变换所以先对矩阵每一位做 FWT,然后再求 det,优化了时间复杂度。因为生成树个数很多,所以我们每时每刻要 \(\bmod\) 一个大质数,错误率很低。时间复杂度 \(O(n^22^ww+n^32^w)\),为什么可以信仰跑过……
没写代码。
AT_abc367_g [ABC367G] Sum of (XOR^K or 0)
和后面几题一样利用 xor FWT 的性质。
这个 \(k\) 次方很烦,逼我们要求出对于不同的异或结果的方案数。
对于异或结果为 \(p\) 的方案 \(f_p=[x^py^0]\prod_{i=1}^N1+x^{A_i}y\),其中 \(x\) 的乘法为异或卷积,\(y\) 的乘法为循环卷积。不能直接模拟,我们对 \(x\) 这一位做 FWT,则 \(FWT[f]_p=[y^0]\prod_{i=1}^N1+c(p,A_i)y\),其中 \(+1\) 是因为对 \(1\) 这个序列做一遍 xor FWT 后每一位都是 \(1\)。
我们可以发现序列 \(x^{A_i}\) 做一遍 FWT,每一位都只能是 \(1\) 或 \(-1\)(由定义可得),我们只需要求出有多少个 \(c(p,A_i)\) 是 \(1\) 就好了,设有 \(cnt_p\) 个,就可以把柿子化成 \(FWT[f]_p=[y^0](1+y)^{cnt_p}(1-y)^{N-cnt_p}\),我们先把 \(cnt_p\) 求出来。因为 FWT 是线性变换(后不赘述了),所以我们只要对 \(\sum_{i=1}^Nx^{A_i}\) 做一遍 xor FWT,就可以对于每一个 \(p\) 求出来 \(\sum_{i=1}^N c(p,A_i)\),解解方程就可以求出来 \(cnt_p\)。
接下来,我们预处理 \((1+y)^x\) 和 \((1-y)^x\) 的每个系数,\(O(nm)\),那么 \(FWT[f]_p=\sum_{i=0}^{m-1}[y^i](1+y)^{cnt_p}\cdot[y^{(m-i)\bmod m}](1-y)^{N-cnt_p}\),后面就很简单了。
时间复杂度 \(O(nm+V(\log V+\log K))\)。
拜谢 TB,TB 太强了。
依旧是需要分别求出不同的异或结果的方案数。对于异或结果为 \(t\) 的方案 \(f_t=[x^t]\prod_{i=1}^n\sum_{j=l_i}^{r_i}x^j\),显然做不了,那就求 \(FWT[f]_t=\prod_{i=1}^n\sum_{j=l_i}^{r_i}(-1)^{t\circ j}=\prod_{i=1}^np_{t,r}-p_{t,l-1}\),其中 \(p_t\) 是前缀和数组,
我们令 \(p\) 数组右移一位,并让 \(l,r\) 分别加一。让每个 \(p_{t,x}\) 划分为若干个 \([a,a+2^w)\) 区间求总和,比如说 \(11010_2\) 就划分成 \([0,0+10000_2),[10000_2,10000_2+1000_2),[11000_2,11000_2+10_2)\),设 \(c\) 为 \(t\) 中前 \(w\) 位 \(1\) 的个数,\(t'\) 为去掉前 \(w+1\) 位后的 \(t\)(为什么是 \(w+1\) 位,因为根据划分方式此时 \(a\) 的前 \(w+1\) 位都是 \(0\)),显然 \(p_{t,x}=\sum_{a,w,c}(-1)^{t'\circ a}2^{w-c}\sum_{i=0}^{c}(-1)^i\binom{c}{i}=\sum_{a,w,c}(-1)^{t'\circ a}2^{w}[c=0]\),我们忽略 \((-1)^{t'\circ a}\),发现同一个 \(m=lowbit_t\),他们的 \(p_t\) 数组是一样的。
我们按照 \(m\) 分类,于是 \(FWT[f]_t=\prod_{i=1}^n(-1)^{t\circ r}a_i-(-1)^{t\circ(l-1)}b_i\),其中 \(a_i,b_i\) 为只保留前 \(m\) 位的 \(r,l-1\),如果 \(a_i,b_i\) 的第 \(m\) 位有数那么要额外减去 \(2^{m+1}\),因为贡献算反了。然后可以把 \(-\) 换成 \(+\),\(b_i\) 取负。把形式换成 \(f_t=\prod_{i=1}^na_ix^{r}+b_ix^{l-1}=\prod_{i=1}^nx^{r}\prod_{i=1}^na_i+b_ix^{r\oplus (l-1)}\),发现后半部分是经典形式,前半部分只需要算出 \(f_i\) 后偏移 \(\prod_{i=1}^nx^{r}\) 位就好了,所以我们求后半部分。
对后半部分 FWT,用类似于 FWT 的方式,设两个数组 \(g_i,h_i\) 表示上面的式子中 \(b_i\) 前面是 \(+,-\) 对 \(FWT[f]_i\) 的贡献,可以发现有 \(x\) 的那部分贡献取负可以快捷地用另外一个数组。最终 \(FWT[f]_i=g_i\),这种思路就相当于是区间状态取反,只需要线段树内提前维护好取反后的信息是怎么样的,就可以 \(O(log)\) 更新查询。
转移:\(g_i=g_i*g_j,h_i=h_i*h_j,g_j=g_i*h_j,h_j=h_i*g_j\)。
没写代码
AT_arc198_e [ARC198E] Monotone OR
这个 \(+1\) 很烦,考虑分成两个状态 \(f_i=g_{i-1},g_i=\sum_{j=1}^M\sum_{s_j\cup k=i}f_k\)。
设 \(a_i=\sum_{j=1}^M[s_j\subseteq i]\),我们容斥得出 \(g_i=a_i\sum_{j\subseteq i}f_j-\sum_{j\subset i}g_j\),半在线求 \(f,g\) 的高维前缀和,像 FWT 那样分治,顺便计算 \(a_i\)。
CF1336E2 Chiori and Doll Picking (hard version)
神仙题,看了?h。
参考 memset0 的题解。
设 \(A=\{v_1,v_2,\dots,v_{|A|}\}\) 为 \(a\) 的线性基,\(k=|A|\)。
\(span(X)=\{c_1 v_1\oplus c_2 v_2\oplus\dots \oplus c_{|X|} v_{|X|} | c_1,c_2,\dots,c_{|X|}\in{0,1}\}\)。
\(F(X)=\sum_{x\in span(X)}z^x\)
可得 \(F(A)*z^x=F(A),x\in span(A)\)
所以当 \(k \le \frac{m}{2}\) 时,直接枚举 \(x\in span(A)\) ,然后对答案额外乘以 \(2^{m-k}\) 就做完了。
当 \(k > \frac{m}{2}\) 时,我们想要一个 \(O(2^{m-k})\) 的做法。
由上面的式子可得
所以 \([z^i]FWT(F(A))\in{0,2^k}\)。
定义 \(A\) 的正交线性基为 \(B\),使得对于所有 \(x\in span(A),y\in span(B)\),满足 $ \text{popcount}(x$ \(\&\) \(y)\) 是偶数,且 \(|A|+|B|=m\)。
由神秘的高等知识可得 \(span(B)\) 是唯一的并且,\(F(B)\cdot 2^k=FWT(F(A))\)。
真要证明就看这个 https://www.luogu.me/article/36svvbai 或者官解吧。
一种简单的正交线性基构造方式是
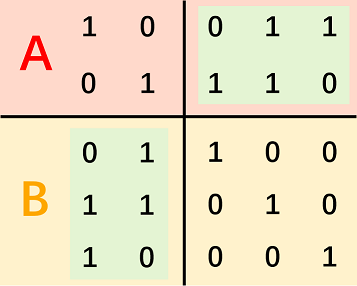
用高斯消元弄出 \(A\) 的那两行,旋转右上角到左下角得到。
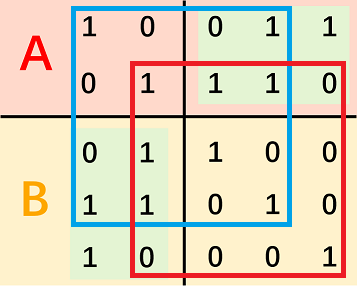
证明可以考虑图中圈出矩形的左上角和右下角一定为 \(1\),当左下角和右上角的数要么全为 \(0\),要么全为 \(1\) 时,上下任意两个数 \(\text{popcount}(x\& y)\) 都为偶数。
当上下任意两个数 \(\text{popcount}(x\& y)\) 都为偶数时,\(∀x∈span(A),∀y∈span(B),\text{popcount}(x\& y)\) 为偶数。证明:
\(x=\{c_1 v_1\oplus c_2 v_2\oplus\dots \oplus c_{|A|} v_{|A|}\},y=\{d_1 w_1\oplus d_2 w_2\oplus\dots \oplus d_{|B|} w_{|B|}\}\),由 \((x\oplus y)\&z=x\&z\oplus y\&z\) 可得 \(x\&y=\oplus_{i}\oplus_{j}v_i\&w_j\),当 \(\text{popcount}(x),\text{popcount}(y)\) 都为偶数时,\(\text{popcount}(x\oplus y)\) 也为偶数。
后面的就可以去吃洛谷题解了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号