集合定义
集合(Set)是一种用来装东西的容器,它所装的东西叫元素(Element)。
集合里的元素,它们可以是任何类型的数学对象:数字、符号、变量、空间中的点、线、面,甚至是其他集合。
规定(书写约定):
-
元素通常用 a, b, c, d, x等小写字母来表示; -
而
集合通常用A, B, C, D, X等大写字母来表示。 一些大写字母已经约定俗成地表示为某类数,比如下面是一些前人已约定好的集合,看到Q就知道是表示有理数:- N——自然数
- Q——有理数
- R——实数
- I——虚数
- C——复数
- .......
集合三特性
无序性:
一个集合中,每个元素的地位都是相同的,元素之间是无序的。
集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
互异性:
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。
有时需要对同一元素出现多次的情形,可以使用多重集,多重集会记录元素出现的次数。
确定性:
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
Tip: 任何编程语言里的集合结构实现,都遵循上述的集合三特性。
集合的表示法—如何描述元素
集合的表示无非是想给这个容器定义好边界、大小,让人能一眼看出它里面能装多少个多大、多小的数字。
常见的表示方式:
-
列举法
直接罗列全部出来,比如:{1,2,3} -
韦恩图法
就是通过用画圈来表示集合,下面有展示。 -
描述法
可以用文字描述,比如: A = 大于零的前三个自然数
也可以用数学符号描述,比如: A ={x|x>0 且 x<4}常见的描述符号(需熟记于心):

元素与集合的关系
元素与集合的关系只有两种,不存在其他情况:
- 属于 ∈
- 不属于 ∉
集合间的关系
集合间的符号:
- 相等 = 、不相等 ≠
- 包含 ⊆ 、不包含 ⊄
- 真包含 ⫋
空集 ∅ 、 {}
就是说这个集合里面什么都不包含。
子集 (Subset)

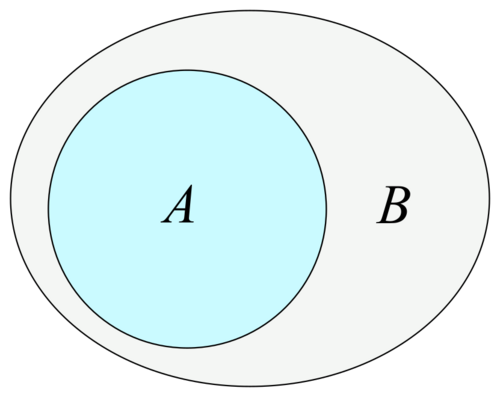
符号类似 A ≤ B
包含关系指的是一种子集关系。具体来说,如果集合A的每一个元素都是集合B的元素,并且集合B中存在至少一个元素不属于集合A,那么我们就可以说集合A包含于集合B,或者集合B包含A。
记作:A ⊆ B ,
读作: A 包含于 B(或 B包含A)。
注意:这个包含于 和 包含 有很大区别!
这里还衍生出 真子集、超集/母集 概念。
等集

全集(Universal Set) U
Tip: 全集的符号是大写英语字母 U ,他很容易和并集的符号 ∪ 混淆。要小心!
-
全集是指在特定上下文中涵盖了所有讨论范围内元素的集合。
-
全集通常用符号U表示。在不同的领域和问题中,会改变符号代称。
简而言之:全集是什么元素都有的集。不是真的什么都有, 只是理论上假设它都有,为了方便描述而已。
注意,全集不是超集,它是一种抽象的描述一个更大范围的方式。
幂集(Power Set) P(A)
幂集是指一个集合所有子集的集合。换句话说,给定一个集合A,幂集P(A)是由A的所有可能子集所构成的集合。
例如,对于集合A = {1, 2},它的幂集P(A)包含以下子集:
P(A) = {∅, {1}, {2}, {1, 2}}
其中,∅表示空集,{1}表示只包含元素1的子集,{2}表示只包含元素2的子集,{1, 2}表示包含元素1和元素2的子集。
集合间的运算
集合的运算律
- 交换律、结合律、分配律
- 德摩根定律
案例背景
S 代表踢足球的人的集
T 代表打网球的人的集
V 代表打排球的人的集
并集(∪)
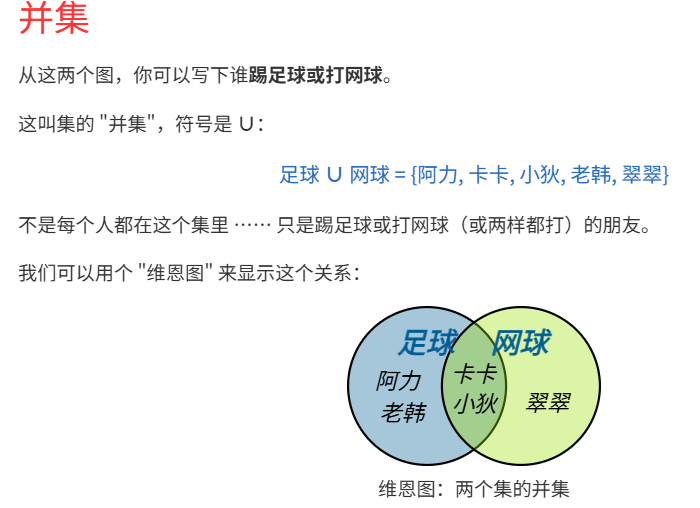
交集(∩)
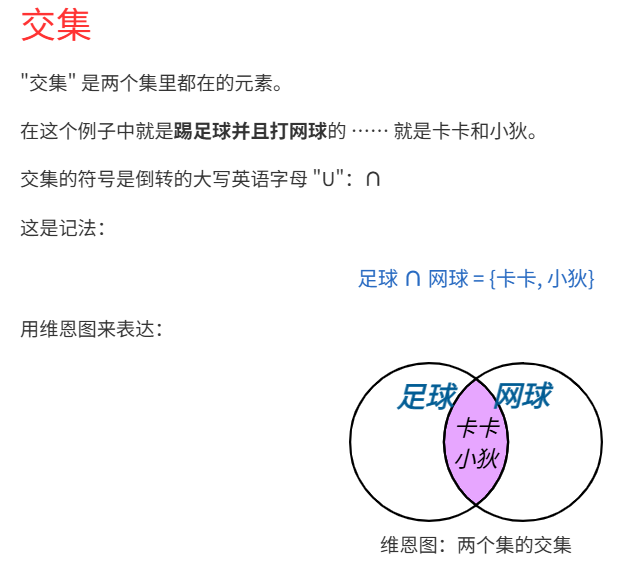
怎么记忆交集和并集?

差集(A - B)

补集 ( C )
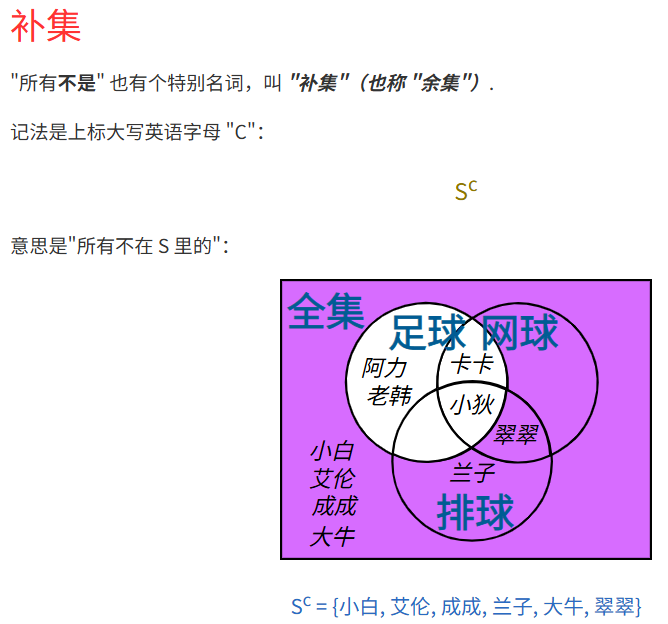




 浙公网安备 33010602011771号
浙公网安备 33010602011771号