滚......

[ARC168F] Up-Down Queries

这题出的很好。
看起来像个复合函数题，然而如果直接做的话似乎不是很能做。不过有一些性质是容易发现的。
首先，令第 \(i\) 个建筑高 \(y_i\)，则 \(y_i\) 单调不降。

因为一次操作可以看成给 \([x_i+1,m]\) 后缀 \(+2\)，然后全局 \(-1\) 再和 \(0\) 取 \(\max\)。归纳一下会发现上述性质是对的。当然直接做也可以，不过这样对接下来的转化有好处。尤其是这个 \(-1\) 由前缀 \(-1\) 变成了全局 \(-1\)。

这启示我们利用差分数组。令 \(y_0=0\)，\(d_i=y_i-y_{i-1}\)，则所求为 \(\sum\limits_{i=1}^n d_i(m-i+1)\)。由于对于每个 \(i\) 来说，\(m-i+1\) 为定值，我们可以把它看成一个多重集里有 \(d_i\) 个 \(m-i+1\)，答案即为多重集的和。（究竟是怎么想到的。）

现在，操作对多重集的影响是什么呢？

后缀加，显然就是把 \(d_{x_i+1}\) 加上 \(2\)。也就是在集合里插入两个 \(m-(x_i+1)+1\) 即 \(m-x_i\)。

全局 \(-1\) 后和 \(0\) 取 \(\max\)。这其实相当于一个后缀减，哪个后缀呢？\(a\) 中第一个非 \(0\) 数对应的后缀。发现 \(a\) 中第一个非 \(0\) 数和 \(d\) 中第一个非 \(0\) 数位置相同，设其位置为 \(i\)。则显然，这个操作就是将 \(d_i\) 减去 \(1\)。不过我们不需要真的把 \(i\) 找出来，因为这个减有特殊性质：它一定对应着删去多重集里的最大值。这是显然的。

于是乎，我们就需要维护两种操作：

1. 插入两个 \(m-x_i\)。
2. 删去集合中的最大值（只删一个）。

删除操作时集合不可能为空，因为这俩操作成对出现。

这咋做呢？

考虑我不知道为啥经典的 Trick，把删除最大值变成删除任意值，让最后多重集的和最小。
看起来很对，但是我觉得要分析一个问题等价。不过我想了一下发现这比较显然，反正就是证新问题答案小于等于原问题答案，然后原问题的操作放在新问题上也合法就可以了。我就不写了。
不是这实在太显然了。

然后我们发现这个问题居然可以费用流！！！

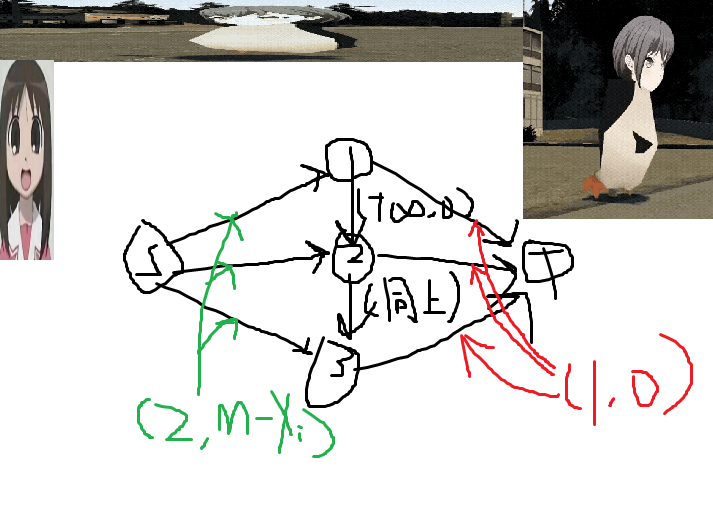
大概就是这样的，有点像餐巾计划。
费用流，可以用来模拟。
除了直接模拟，还有一种做法是先确定一个最大流再增广环。这非常好，因为这个图的最大流很显然，\(S\) 到 \(i\) 再到 \(T\) 就行了。
我们假设初始 \(x_i\) 都是 \(m\)，把题目输入的序列当作修改。每次增广一个环，我都是不可能经过连向汇点的边的，因为有出必有进，那么必定有一个方向的这种边满流了。于是我的增广就只有可能经过图的中间和左半部分。我要修改 \(x_i\)，那就只需要尝试增广经过 \((S,i)\) 的环。

假设这是一个 \([S,i,j,S]\) 的环（符号乱用的），\(i\neq j\)，那么代价为 \(+(m-x_i)-(m-x_j)\)，即 \(x_j-x_i\)。所以这种增广，我只需要找到有流量的 \(j\) 中 \(x_j\) 最大的。（有没有流量指的是 \((S,j)\) 有没有流量，这个可以修改时维护。）

假设这是一个 \([S,j,i,S]\) 的环（符号乱用的），\(j\neq i\)，那么代价为 \(+(m-x_j)-(m-x_i)\)，即 \(x_i-x_j\)。反正是一样的吧。只用找没满流的 \((S,j)\) 就行了。

然后好像就做完了吧。这个增广次数理论上也不会太多。我如果退了 \((S,i)\) 又流了 \((S,i)\)，那么本质上是在操作另外一个环，如果真的有正贡献，那在之前就应该做了，不会拖到现在，所以不会出现这种情况。

这些东西全部线段树维护就可以了。需要注意的是，维护的答案也要根据 \((S,i)\) 流量的多少实时修改。然后就真的做完了。时间复杂度 \(O(n\log n)\)。

UPD：居然有问题。想退流时还需要保证 \(+\infty\) 链上可以退。再开一棵线段树维护。

比如第一种环，\(i<j\)，那么啥限制都没有。但是如果 \(i>j\)，那么就必须满足中间全部有流量。这个再开一个线段树二分一下就行了。

P9167 [省选联考 2023] 城市建造

哈喽小伙伴们大家好，今天我们要挑战的是省选联考 2023 D1T2，觉得我能过的小伙伴们直播间“666”刷起来。

求你们不要再出这种点双/边双题了。什么建造军营、建造军营2、电动力学、咕咕嘎嘎，这都是什么乱七八糟的。又来一个什么城市建造。你就建造吧。

首先，这个条件给的比较抽象，它有许多相同的表述。比如说，我选 \(t\) 个点，将它们之间的连边全部删去，最后得到 \(t\) 个连通块，且它们的大小极差 \(\leq k\)，那这个和原条件是等价的。什么意思呢？就是它给的形式化题意中，我们确定了 \(E'\) 的话，其实是可以确定 \(V'\) 的。但相反，确定了 \(V'\)，我们也可以确定 \(E'\)。因此我们考虑对于 \(V'\) 来计数。

显然，选择的 \(t\) 个点最后必须属于不同的连通块，而且它们最初一定连通。这都是可以证明的。假设存在 \(u,v\in V'\)，\(w\notin V'\)，且 \(u,v,w\) 同属一个点双，那么根据定义，一定存在 \(u\) 到 \(w\) 再到 \(v\) 的路径，这和前面所说冲突了。这启示我们，一个点双里要么全选，要么只选一个，要么不选。而且只选一个也只能选割点，因为 \(t\neq 1\)，且点集 \(V'\) 在原图上必须通过 \(V'\) 之间的边连通。所以把圆方树建出来，选择的一定是若干个连续的方点。选择一个方点代表在 \(V'\) 中加入这个方点周围所有的圆点，连续意为任意两个选择的方点路径上的方点都要选择。

当一个方点被选择，它的所有连边就需要被删除，此时，这个点双里的点一定全部不连通。对于一个非割点来说，它的连通块大小此时必定为 \(1\) 了。但是对于割点来说，它的连通块大小此时必定 \(>1\)（除非它所在的其它点双也被选择）。这个不重要，我乱说的。反正就是，一个选择方案合法，当且仅当其形成的所有连通块圆点个数极差不超过 \(k\)。

那这个怎么做啊？可以先枚举连通块大小 \(t\)。若 \(k=0\)，那连通块大小必定是 \(n\) 的因数。若 \(k=1\)，设连通块个数是 \(cnt\)，那连通块大小必定是 \(\lfloor\frac{n}{cnt}\rfloor\) 或 \(\lceil\frac{n}{cnt}\rceil\)。所以 \(t\) 只有 \(O(\sqrt n)\) 个，而且 \(\sum t\) 是 \(O(n\log n)\) 量级的。于是可以直接树形背包做到 \(O(n\sum t)\) 即 \(O(n^2\log n)\)。

格老子的格老子的格老子的格老子的格老子的。
格老子的格老子的格老子的格老子的格老子的。
格老子的格老子的格老子的格老子的格老子的。

A. 区间计数

D1T1。非常困难。

显然，寻找一个简单的刻画两个区间相等的条件是重要的。现在我们考虑判断区间 \([l1,r1]\) 和 \([l2,r2]\) 是否相等（\(r1<l2\)）。
令 \(b_i\) 表示 \(a_i\) 上一次出现时的下标。若 \(a_i\) 第一次出现，则 \(b_i=-2i\)。令 \(br(l,r)=\max(0,\max\limits_{i=l}^r b_i)\)，\(bl(l,r)=\min\limits_{i=l}^r b_i\)。那么 \([l1,r1]\) 和 \([l2,r2]\) 相等的充要条件为：

• \(bl(l2,r2)=l1\)。
• \(br(l2,r2)=r1\)。

这应该相当显然。
通过这一点，我们可以想到找到所有存在 \([l1,r1]\) 的 \([l2,r2]\)，我们称这些 \([l2,r2]\) 为关键区间。

\([l,r]\) 是关键区间，当且仅当 \(br(l,r)-bl(l,r)-(r-l)=0\)。

这应该也相当显然。简单说明一下。

• \([l,r]\) 中的数全部是第一次出现。

  原式等于 \(0-(-2r)-(r-l)=l+r > 0\)。

• \([l,r]\) 中的数有第一次出现的，也有第二次出现的。

  （此处证明询问了 DeepSeek。）

  令 \(A=\{i\in[l,r],b_i<0\}\)，\(B=\{i\in[l,r],b_i>0\}\)。那么 \(-bl(l,r) = -(-2\max A)=2\max A\)。设 \(M_A=\max A\)。

  然后令 \(M_B=br(l,r)\)，易知 \(M_B\geq |B|\)。

  所以有原式等于 \(M_B+2M_A-(r-l)\)。分析其下界。
  易知 \(M_A\geq l+|A|-1\)，且 \(|A|+|B|=r-l+1\)，所以 \(|A|=r-l+1-|B|\)，即 \(M_A\geq r-|B|\)，于是有 \(2M_A\geq 2r-2|B|\)。

  下界全部代入，得到原式大于等于 \(|B|+2r-2|B|-(r-l)=r+l-|B|\)。由条件，\(1\leq |B|\leq r-l\)，所以 \((r+l-|B|)_{\min}=2l\geq 2\)。因此此时原式一定大于等于 \(2\)。

• \([l,r]\) 中的数全部是第二次出现。
  最简单的。

所以这条件是充要的，而且设 \(E(l,r)=br(l,r)-bl(l,r)-(r-l)\)，那么一定有 \(E(l,r)\geq 0\)。

我累了，怎么写了这么久只写了这么一点。

B. 赫露艾斯塔