二叉树刷题总结
530. 二叉搜索树的最小绝对差
二叉搜索树的特点,左边<根<右,有一个特点,就是中序遍历是有序的(二叉搜索树的中序遍历序列是升序的),这里如何记忆前,中和后序,就理解根在三个中的那个位置,前序就是收尾
我们在二叉搜索树中获取有序数据仅需 O(n)时间,无须进行额外的排序操作,非常高效。
/* 前序遍历 */
void preOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:根节点 -> 左子树 -> 右子树
list.add(root.val);
preOrder(root.left);
preOrder(root.right);
}
/* 中序遍历 */
void inOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:左子树 -> 根节点 -> 右子树
inOrder(root.left);
list.add(root.val);
inOrder(root.right);
}
/* 后序遍历 */
void postOrder(TreeNode root) {
if (root == null)
return;
// 访问优先级:左子树 -> 右子树 -> 根节点
postOrder(root.left);
postOrder(root.right);
list.add(root.val);
}
基于上面的特点,计算最小的绝对值差,转变为比较相邻元素的差值
class Solution {
private int ans = Integer.MAX_VALUE;
private Integer prev = null; // 前驱值,初始为空
public int getMinimumDifference(TreeNode root) {
inorder(root);
return ans;
}
private void inorder(TreeNode node) {
if (node == null)
return;
inorder(node.left);
if (prev != null) // 已有前驱
ans = Math.min(ans, node.val - prev);
prev = node.val; // 更新前驱
inorder(node.right);
}
}
数组表示二叉树
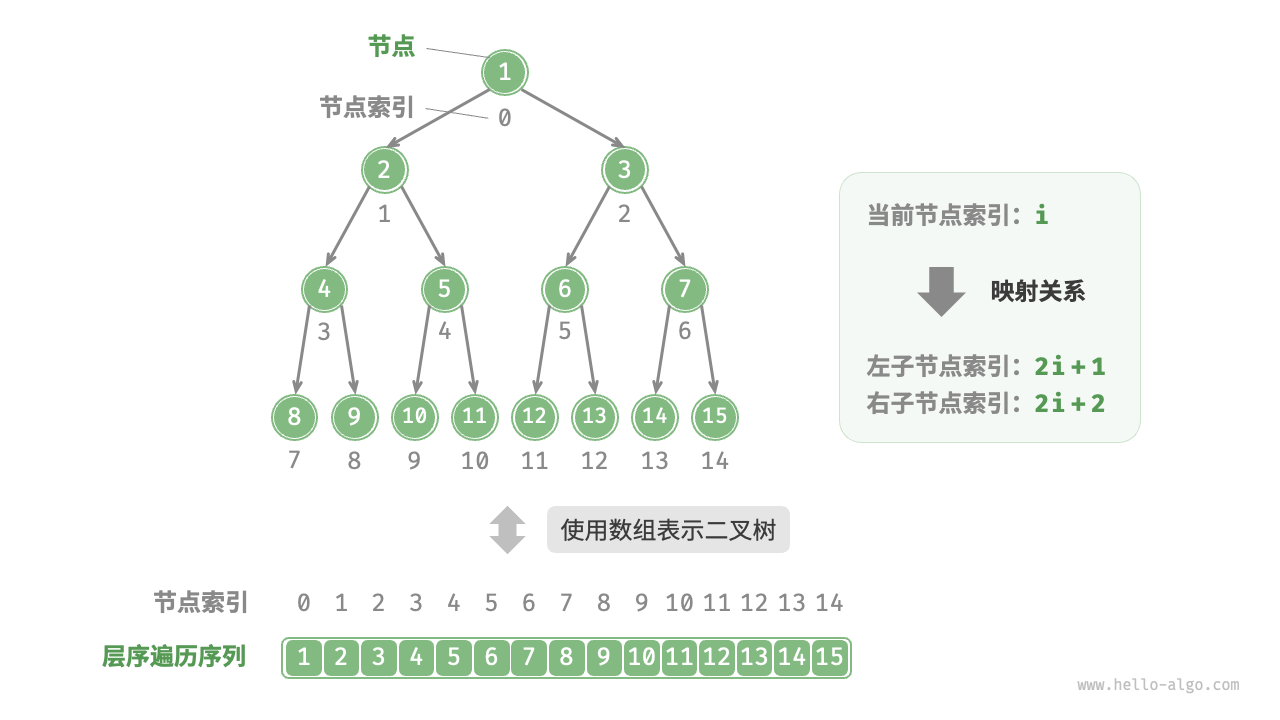
/* 数组表示下的二叉树类 */
class ArrayBinaryTree {
private List<Integer> tree;
/* 构造方法 */
public ArrayBinaryTree(List<Integer> arr) {
tree = new ArrayList<>(arr);
}
/* 列表容量 */
public int size() {
return tree.size();
}
/* 获取索引为 i 节点的值 */
public Integer val(int i) {
// 若索引越界,则返回 null ,代表空位
if (i < 0 || i >= size())
return null;
return tree.get(i);
}
/* 获取索引为 i 节点的左子节点的索引 */
public Integer left(int i) {
return 2 * i + 1;
}
/* 获取索引为 i 节点的右子节点的索引 */
public Integer right(int i) {
return 2 * i + 2;
}
/* 获取索引为 i 节点的父节点的索引 */
public Integer parent(int i) {
return (i - 1) / 2;
}
/* 层序遍历 */
public List<Integer> levelOrder() {
List<Integer> res = new ArrayList<>();
// 直接遍历数组
for (int i = 0; i < size(); i++) {
if (val(i) != null)
res.add(val(i));
}
return res;
}
/* 深度优先遍历 */
private void dfs(Integer i, String order, List<Integer> res) {
// 若为空位,则返回
if (val(i) == null)
return;
// 前序遍历
if ("pre".equals(order))
res.add(val(i));
dfs(left(i), order, res);
// 中序遍历
if ("in".equals(order))
res.add(val(i));
dfs(right(i), order, res);
// 后序遍历
if ("post".equals(order))
res.add(val(i));
}
/* 前序遍历 */
public List<Integer> preOrder() {
List<Integer> res = new ArrayList<>();
dfs(0, "pre", res);
return res;
}
/* 中序遍历 */
public List<Integer> inOrder() {
List<Integer> res = new ArrayList<>();
dfs(0, "in", res);
return res;
}
/* 后序遍历 */
public List<Integer> postOrder() {
List<Integer> res = new ArrayList<>();
dfs(0, "post", res);
return res;
}
}
230. 二叉搜索树中第 K 小的元素
思路整理:对于搜索树,使用中序遍历即可,维护一个计数器,来记录第几个元素,一旦发现访问到了第k个元素,直接赋值,然后返回即可。
class Solution {
int res = -1;
int index = 0; // 0->k-1次遍历
public int kthSmallest(TreeNode root, int k) {
// 中序遍历
dfs(root, k);
return res;
}
public void dfs(TreeNode root, int k) {
if (root == null) {
return;
}
dfs(root.left, k);
index++;
if (index == k) {
res = root.val;
return;
}
dfs(root.right, k);
}
}
98. 验证二叉搜索树
二叉搜索树,进行中序遍历,是否满足前一个元素,小于后一个元素,如果不满足,那么就不是
class Solution {
Integer prev = null;
boolean res = true;
public boolean isValidBST(TreeNode root) {
inorder(root);
return res;
}
public void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
if (prev != null) {
if (prev < root.val) {
// doNothing
} else {
res = false;
}
}
if (!res) {
return;
}
prev = root.val;
inorder(root.right);
}
}
105. 从前序与中序遍历序列构造二叉树
先序遍历的顺序是根节点,左子树,右子树。中序遍历的顺序是左子树,根节点,右子树。
所以我们只需要根据先序遍历得到根节点,然后在中序遍历中找到根节点的位置,它的左边就是左子树的节点,右边就是右子树的节点。
生成左子树和右子树就可以递归的进行了。
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildTreeHelper(preorder, 0, preorder.length, inorder, 0, inorder.length, map);
}
private TreeNode buildTreeHelper(int[] preorder, int p_start, int p_end, int[] inorder, int i_start, int i_end,
HashMap<Integer, Integer> map) {
if (p_start == p_end) {
return null;
}
int root_val = preorder[p_start];
TreeNode root = new TreeNode(root_val);
int i_root_index = map.get(root_val);
int leftNum = i_root_index - i_start;
root.left = buildTreeHelper(preorder, p_start + 1, p_start + leftNum + 1, inorder, i_start, i_root_index, map);
root.right = buildTreeHelper(preorder, p_start + leftNum + 1, p_end, inorder, i_root_index + 1, i_end, map);
return root;
}
}
106. 从中序与后序遍历序列构造二叉树
关于为什么使用开区间避免数组越界的解释:
把区间写成「左闭右开」[first, last) 并不是语法强制,而是一种人为约定的编程习惯。它之所以「看起来能避免越界」,核心原因是:
把「越界检查」从「两个不同的判等」变成「一个统一的比较」,从而减少差一错误。
1. 数学视角:长度直接可算
[first, last) 的元素个数 = last − first
不需要再 +1 或 −1,一眼就能看出长度。
在递归里经常要根据「左子树节点数」去切分数组,用左闭右开时:
左子树节点数 = idx − iStart // 正好就是长度
右子树节点数 = iEnd − (idx+1)
2. 终止条件统一
if (first == last) → 空区间
无论是空数组、单元素、还是多元素,统一只判相等即可。
如果是闭区间 [first, last],你就得写:
if (first > last) → 空
多了一种「>` 情况,容易把边界写错。
3. 与 Java/C++ 标准库保持一致
- Java 的
Arrays.copyOfRange(arr, from, to)→ 复制[from, to) - C++ 的
std::vector::begin()/end()→ 迭代器区间也是左闭右开 - Python 的
s[a:b]→ 同样含左不含右
跟着标准库走,别人读你的代码时零成本理解。
4. 越界故事的本质
数组合法下标范围是 0 … length-1。
采用左闭右开后,last 正好可以取到 length,而 length 本身不需要被解引用,它只是「哨兵」:
[0, length) → 下标 0 … length-1 安全
[0, length] → 还想访问下标 length 瞬间越界
因此「避免越界」并不是魔法,而是:
把「越界值」当成区间终点,但永远不访问它。
5. 一张小表格总结
| 区间表示 | 空区间判断 | 长度计算 | 是否易错 |
|---|---|---|---|
| [i, j) | i == j | j − i | 低 |
| [i, j] | i > j | j − i +1 | 高 |
6. 结论(一句话背下来)
左闭右开不是语法,是习惯;
它把「长度、空区间、切分」全部统一到减法+等号,
于是差一错误显著减少,看起来就「不会越界」了。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return dfs(inorder, 0, inorder.length , postorder, 0, postorder.length , map);
}
public TreeNode dfs(int[] inorder, int iStart, int iEnd, int[] postorder, int pStart, int pEnd,
Map<Integer, Integer> map) {
if (pStart == pEnd) {
return null;
}
int rootVal = postorder[pEnd - 1];
int index = map.get(rootVal);
int num = index - iStart;
TreeNode root = new TreeNode(rootVal);
root.left = dfs(inorder, iStart, index, postorder, pStart, pStart + num, map);
root.right = dfs(inorder, index + 1, iEnd, postorder, pStart + num, pEnd - 1, map);
return root;
}
}
117. 填充每个节点的下一个右侧节点指针 II
这个题目简单思考一个就可以想出来,使用层序遍历的方式去处理,while中使用for循环,去遍历当前这一层的元素,找到最后一层元素后,直接prev.next=null即可,注意不处理null值
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null) {
return root;
}
// 层序遍历二叉树
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
Node prev;
while(queue.size() > 0) {
int times = queue.size();
prev = queue.poll();
add(prev, queue);
for(int i = 1; i < times; i++) {
Node cur = queue.poll();
add(cur, queue);
prev.next = cur;
prev = cur;
}
prev.next = null;
}
return root;
}
public void add(Node node, Queue queue) {
if (node == null) {
return;
}
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
114. 二叉树展开为链表
自己就做出来的简单算法,使用一个列表来存储索引的节点,然后遍历这个列表,left置为null,right置为下一个节点即可。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
List<TreeNode> list = new ArrayList<TreeNode>();
public void flatten(TreeNode root) {
if (root == null) {
return;
}
inorder(root);
TreeNode prev = root;
for (int i = 1; i < list.size(); i++) {
TreeNode cur = list.get(i);
prev.left = null;
prev.right = cur;
prev = cur;
}
}
public void inorder(TreeNode root) {
if (root == null) {
return;
}
list.add(root);
inorder(root.left);
inorder(root.right);
}
}
能否不适应列表来解决这个问题?
使用一个栈,每次去现去left,也就是说left先压入栈,代码如下:
class Solution {
public void flatten(TreeNode root) {
if (root == null) {
return;
}
Deque<TreeNode> stack = new LinkedList<TreeNode>();
stack.push(root);
TreeNode prev = null;
while (!stack.isEmpty()) {
TreeNode curr = stack.pop();
if (prev != null) {
prev.left = null;
prev.right = curr;
}
TreeNode left = curr.left, right = curr.right;
if (right != null) {
stack.push(right);
}
if (left != null) {
stack.push(left);
}
prev = curr;
}
}
}
第三种方法:
对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束。
class Solution {
public void flatten(TreeNode root) {
TreeNode curr = root;
while (curr != null) {
if (curr.left != null) {
TreeNode next = curr.left;
TreeNode predecessor = next;
while (predecessor.right != null) {
predecessor = predecessor.right;
}
predecessor.right = curr.right;
curr.left = null;
curr.right = next;
}
curr = curr.right;
}
}
}
作者:力扣官方题解
链接:https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/solutions/356853/er-cha-shu-zhan-kai-wei-lian-biao-by-leetcode-solu/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
173. 二叉搜索树迭代器
这个解题其实很简单:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class BSTIterator {
List<Integer> list = new ArrayList<>();
int size = 0;
int index = 0;
public BSTIterator(TreeNode root) {
inorder(root);
size = list.size();
}
void inorder(TreeNode root) {
if (root == null) {
return;
}
inorder(root.left);
list.add(root.val);
inorder(root.right);
}
public int next() {
int val = list.get(index);
index++;
return val;
}
public boolean hasNext() {
return index < size;
}
}
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator obj = new BSTIterator(root);
* int param_1 = obj.next();
* boolean param_2 = obj.hasNext();
*/
迭代版本的二叉树遍历
class Solution {
List<Integer> ans = new ArrayList<>();
Deque<TreeNode> d = new ArrayDeque<>();
public List<Integer> inorderTraversal(TreeNode root) {
while (root != null || !d.isEmpty()) {
// 步骤 1
while (root != null) {
d.addLast(root);
root = root.left;
}
// 步骤 2
root = d.pollLast();
ans.add(root.val);
// 步骤 3
root = root.right;
}
return ans;
}
}
作者:宫水三叶
链接:https://leetcode.cn/problems/binary-search-tree-iterator/solutions/684405/xiang-jie-ru-he-dui-die-dai-ban-de-zhong-4rxj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
对于上面的题目,就可以这么解题了
class BSTIterator {
// 这里是用来多栈的,先进先出,先加入left,假如到无法假如为止
Deque<TreeNode> d = new ArrayDeque<>();
public BSTIterator(TreeNode root) {
// 步骤 1
dfsLeft(root);
}
public int next() {
// 步骤 2
TreeNode root = d.pollLast();
int ans = root.val;
// 步骤 3
root = root.right;
// 步骤 1
dfsLeft(root);
return ans;
}
void dfsLeft(TreeNode root) {
while (root != null) {
d.addLast(root);
root = root.left;
}
}
public boolean hasNext() {
return !d.isEmpty();
}
}
作者:宫水三叶
链接:https://leetcode.cn/problems/binary-search-tree-iterator/solutions/684405/xiang-jie-ru-he-dui-die-dai-ban-de-zhong-4rxj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
236. 二叉树的最近公共祖先
我自己的解法:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
TreeNode res;
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
postOrder(root, p, q);
return res;
}
public Integer postOrder(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || res != null) {
return null;
}
// 左边是否都满足
Integer case1 = postOrder(root.left, p, q);
if (case1 != null && case1 == 2) {
return 2;
}
// 右边的满足情况
Integer case2 = postOrder(root.right, p, q);
if (case2 != null && case2 == 2) {
return 2;
}
if (case1 == null && case2 == null) {
if (root.val == p.val || root.val == q.val) {
return 1;
} else {
return null;
}
}
if (case1 == null || case2 == null) {
if (root.val == p.val || root.val == q.val) {
res = root;
return 2;
}
return 1;
}
res = root;
return 1;
}
}
不够优雅
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
// 递归终止条件:找到目标节点或空节点
if (root == null || root == p || root == q) {
return root;
}
// 后序遍历左右子树
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 左右子树都找到目标节点 → 当前节点是LCA
if (left != null && right != null) {
return root;
}
// 只在左/右子树找到 → 向上传递找到的节点
return left != null ? left : right;
}
}
新直觉的形成
- 返回值的语义转变 :
- 不再用数字标记状态,而是直接返回 “找到的节点”:
- 若返回
p或q:表示子树中存在目标节点; - 若返回非
p/q的节点:表示该节点是 LCA; - 若返回
null:表示子树中无目标节点。
- 若返回
- 后序遍历的逻辑优势 :
- 先递归左右子树,确保能 “自底向上” 判断:
- 当左右子树同时返回非
null时,当前节点必为 LCA(因为是第一个满足此条件的节点); - 若仅一侧返回非
null,则向上传递该节点(表示目标节点在这一侧)。
- 当左右子树同时返回非
- 消除全局变量 :
- 递归函数本身通过返回值传递结果,无需依赖外部变量,代码更健壮。
对比理解
- 你的代码:通过计数(
1/2)间接判断 LCA; - 优化代码:通过 “是否找到节点” 直接判断 LCA,逻辑更直观。
这种写法的核心是 利用递归的返回值直接传递关键信息 ,而非额外的状态码,符合二叉树问题 “递归 + 后序遍历” 的经典范式。记住这个直觉: LCA 问题中,递归返回值要么是目标节点,要么是 LCA 本身,要么是 null 。
步骤 1:定义递归函数的 “返回值语义”
先想清楚:递归函数要返回什么信息?(比如 LCA 问题中,返回 “找到的目标节点或 LCA”)
步骤 2:确定递归终止条件
- 遇到
null:返回null(子树无目标); - 遇到目标节点(
p或q):返回该节点(找到目标)。
步骤 3:后序遍历处理当前节点
- 递归左子树,得到
left; - 递归右子树,得到
right; - 根据
left和right的组合判断:- 若
left != null && right != null:当前节点是 LCA,返回它; - 若
left != null:返回left(目标在左子树); - 若
right != null:返回right(目标在右子树)。
- 若
108. 将有序数组转换为二叉搜索树
有序数组→BST
数组 本身就是 inorder ,而且 中点就是根 ;不需要再“找根”,也不需要“跨数组映射”。
一句话:区间 [l, r] 里 mid = (l+r)/2 就是根,左边全是左子树,右边全是右子树—— 一条数组、两个指针足够 。
中序+后序:这个看地106题,是不一样的思路,这个地方已经是有序数组,肯定不能用106这道题的解题方法。
数组被根劈成两段,必须先找到根在 inorder 里的下标,才能知道左右子树各自的长度;因此需要 4 个指针(inL, inR, postL, postR)来回映射。
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return build(nums, 0, nums.length - 1);
}
// 一句话记忆:mid 当根,左右分治,l>r 就停
private TreeNode build(int[] nums, int l, int r) {
if (l > r)
return null; // 唯一出口
int mid = l + (r - l) / 2; // 防溢出写法
TreeNode root = new TreeNode(nums[mid]);
root.left = build(nums, l, mid - 1);
root.right = build(nums, mid + 1, r);
return root;
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号