lingqing
第四次作业（凌清2018204196应数一班）
这个作业属于哪个课程 https://edu.cnblogs.com/campus/qdu/DS2020/
这个作业要求在哪里 https://edu.cnblogs.com/campus/qdu/DS2020/homework/11296
这个作业的目标 <掌握两种线性结构：堆栈和队列，和它们分别对应的入栈、出栈及入队、出队操作，以及循环队列的特点及其操作>
学号 2018204196

一、实验目的
1、掌握栈的结构特性及其入栈，出栈操作；
2、掌握队列的结构特性及其入队、出队的操作，掌握循环队列的特点及其操作。

二、实验预习
说明以下概念
1、顺序栈：

  • 顺序栈是栈的顺序实现。顺序栈是指利用顺序存储结构实现的栈。采用地址连续的存储空间（数组)依次存储栈中数据元素，由于入栈和出栈运算都是在栈顶进行，而栈底位置是固定不变的，可以将栈底位置设置在数组空间的起始处；栈顶位置是随入栈和出栈操作而变化的，故需用一个整型变量top来记录当前栈顶元素在数组中的位置。

2、链栈：

  • 链式栈是一种数据存储结构，可以通过单链表的方式来实现，使用链式栈的优点在于它能够克服用数组实现的顺序栈空间利用率不高的特点，但是需要为每个栈元素分配额外的指针空间用来存放指针域。

3、循环队列：

  • 为充分利用向量空间，克服"假溢出"现象的方法是：将向量空间想象为一个首尾相接的圆环，并称这种向量为循环向量。存储在其中的队列称为循环队列（Circular Queue）。循环队列是把顺序队列首尾相连，把存储队列元素的表从逻辑上看成一个环，成为循环队列。

4、链队：

  • 链式队列的实现思想同顺序队列类似，只需创建两个指针（命名为 top 和 rear）分别指向链表中队列的队头元素和队尾元素。

三、实验内容和要求
1、阅读下面程序，将函数Push和函数Pop补充完整。要求输入元素序列1 2 3 4 5 e，运行结果如下所示。

#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define STACK_INT_SIZE 10  /*存储空间初始分配量*/
#define STACKINCREMENT 5  /*存储空间分配增量*/
typedef  int ElemType; /*定义元素的类型*/
typedef struct{
    ElemType *base;
    ElemType *top;
    int stacksize;     /*当前已分配的存储空间*/
}SqStack;

int InitStack(SqStack *S);   /*构造空栈*/
int push(SqStack *S,ElemType e); /*入栈*/
int Pop(SqStack *S,ElemType *e);  /*出栈*/
int CreateStack(SqStack *S);     /*创建栈*/
void PrintStack(SqStack *S);   /*出栈并输出栈中元素*/

int InitStack(SqStack *S){
    S->base=(ElemType *)malloc(STACK_INT_SIZE *sizeof(ElemType));
    //为栈分配空间
    if(!S->base) return ERROR; //分配失败
    S->top=S->base; //初始栈为空
    S->stacksize=STACK_INT_SIZE; //初始大小
    return OK;
}/*InitStack*/

int Push(SqStack *S,ElemType e){
      if (S->top-S->base>=S->stacksize){
      S->base=(ElemType *)malloc((S->stacksize+STACKINCREMENT )*sizeof(ElemType));
      //重新分配空间 
      if(!S->base) return ERROR; //分配失败 
      S->stacksize+=STACKINCREMENT; //大小变化 
      } //栈满 
      *S->top++= e; //先赋值后将top+1
      return OK;    
}/*Push*/

int Pop(SqStack *S,ElemType *e){
      if(S->top == S->base){
      return ERROR;
      } //栈空 
      S->top=--S->top; //top值改变成原来-1 
      *e = *S->top; //存储原来最顶的元素值 
      return OK;   
}/*Pop*/

int CreateStack(SqStack *S){
    int e;
    if(InitStack(S))
        printf("Init Success!\n"); //初始化成功 
    else{
        printf("Init Fail!\n"); //初始化失败
        return ERROR;
    }
    printf("input data:(Terminated by inputing a character)\n");
    while(scanf("%d",&e))
        Push(S,e); //放入元素
    return OK;
}/*CreateStack*/

void PrintStack(SqStack *S){
    ElemType e;
    while(Pop(S,&e))
        printf("%3d",e); //输出出栈的元素
}/*Pop_and_Print*/

int main(){
    SqStack ss;
    printf("\n1-createStack\n");
    CreateStack(&ss);
    printf("\n2-Pop&Print\n");
    PrintStack(&ss);
    return 0;
}

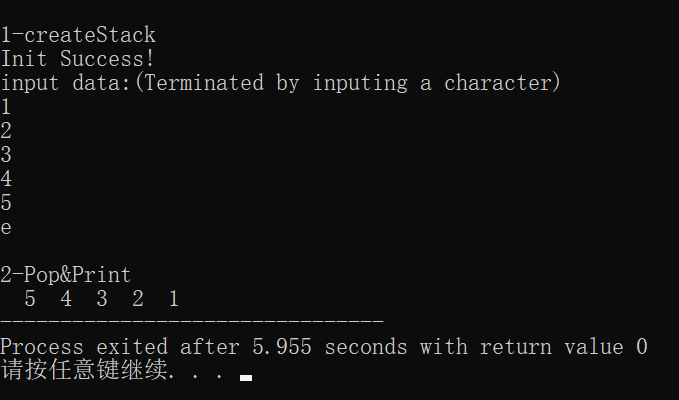
算法分析：输入元素序列1 2 3 4 5，为什么输出序列为5 4 3 2 1？体现了栈的什么特性？

  • 由于入栈和出栈运算都是在栈顶进行，所以将1,2,3,4,5依次压入栈，再将元素弹出栈得到的就是5,4,3,2,1。这体现了栈的后进先出的特点。

2、在第1题的程序中，编写一个十进制转换为二进制的数制转换算法函数（要求利用栈来实现），并验证其正确性。

实现代码

#include<stdio.h>
#include<malloc.h>
#define ERROR 0
#define OK 1
#define STACK_INT_SIZE 10  /*存储空间初始分配量*/
#define STACKINCREMENT 5  /*存储空间分配增量*/
typedef  int ElemType; /*定义元素的类型*/
typedef struct{
    ElemType *base;
    ElemType *top;
    int stacksize;     /*当前已分配的存储空间*/
}SqStack;

int InitStack(SqStack *S);   /*构造空栈*/
int push(SqStack *S,ElemType e); /*入栈*/
int Pop(SqStack *S,ElemType *e);  /*出栈*/
int CreateStack(SqStack *S);     /*创建栈*/
void PrintStack(SqStack *S);   /*出栈并输出栈中元素*/

int t; //
int z=0; //

int InitStack(SqStack *S){
    S->base=(ElemType *)malloc(STACK_INT_SIZE *sizeof(ElemType)); /*为栈分配空间*/ 
    if(!S->base) return ERROR; //分配失败 
    S->top=S->base; //空栈无元素 
    S->stacksize=STACK_INT_SIZE; //初始大小 
    return OK;
}/*InitStack*/

int Push(SqStack *S,ElemType e){
	if (S->top-S->base>=S->stacksize){
		S->base=(ElemType *)malloc((S->stacksize+STACKINCREMENT )*sizeof(ElemType));
		//重新分配空间 
		if(!S->base) return ERROR; //分配失败 
		S->stacksize+=STACKINCREMENT; //大小变化 
		} //栈满 
		*S->top++= e; //先赋值后将top+1
		return OK;
}/*Push*/

int Pop(SqStack *S,ElemType *e){
    if(S->top == S->base){
	return ERROR;
    } //栈空 
	S->top=--S->top; //top值改变成原来-1 
	*e = *S->top; //存储原来最顶的元素值 
	return OK;
}/*Pop*/

int CreateStack(SqStack *S){
    int x; //
	int e;
    if(InitStack(S))
        printf("Init Success!\n"); //初始化成功 
    else{
        printf("Init Fail!\n"); //初始化失败 
        return ERROR;
    }
//    printf("input data:(Terminated by inputing a character)\n");
//    while(scanf("%d",&e))
//    	Push(S,e); //放入元素 
    printf("请输入要转换的十进制整数:"); //
	scanf("%d", &x); //
	t = x; //将输入的数据存储起来为后面做判断 
	while(x/2>0){ //
		e = x%2; // 
		x = x/2; //
        Push(S,e); //
	} //
	Push(S,x);
	return OK;
}/*CreateStack*/


void PrintStack(SqStack *S){
	int a[15]; //定义一个数组存储每一次输出的数值 
    ElemType e;
    int i; //
    int j; //
    int y; //
    i = 0; //
    while(Pop(S,&e)) {
//        printf("%3d",e); //输出出栈的元素 
	printf("%d",e); //输出出栈的元素
	a[i] = e; //将每一次输出的数值存起来为后面做计算验证 
	i++; //
	} //
	for(j=0;j<i;j++){ //
		for(y=0;y<i-1-j;y++){ //
			a[j] = a[j] *2; //
		} //
		z += a[j]; //将得到的转换结果逆运算做十进制转换，所得结果数值赋予z 
	} //
	printf("\n验证所得结果转换为十进制为：%d\n",z); //
}/*Pop_and_Print*/

void CheckStack(SqStack *S){ //
	if(z == t) printf("转换成功！"); //
	else printf("转换失败。"); //
	return; //验证转换的正确性 
} /*CheckStack*/ 

int main(){
    SqStack ss;
    printf("\n1-createStack\n");
    CreateStack(&ss);
    printf("\n2-Pop&Print\n");
    PrintStack(&ss);
    CheckStack(&ss); //
    return 0;
}

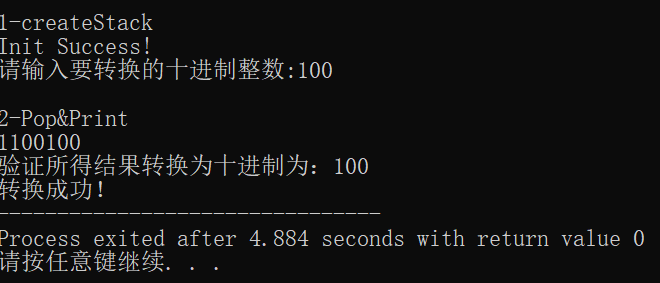
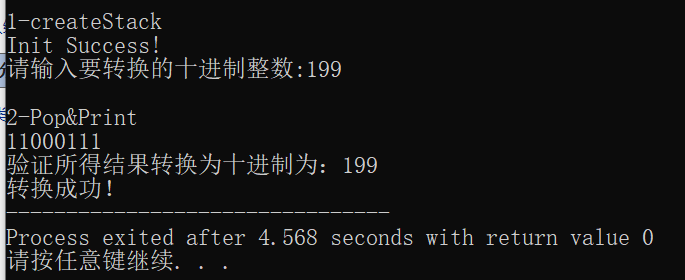
验证

3、阅读并运行程序，并分析程序功能。

#include<stdio.h>
#include<malloc.h>
#include<string.h>
#define M 20
#define  elemtype  char
typedef struct
{
    elemtype stack[M];
    int top;
}
stacknode;
void init(stacknode *st);
void push(stacknode *st,elemtype x);
void pop(stacknode *st);

void init(stacknode *st)
{
    st->top=0;
}

void push(stacknode *st,elemtype x)
{
    if(st->top==M)
        printf("the stack is overflow!\n");
    else
    {
        st->top=st->top+1;
        st->stack[st->top]=x;
    }
}

void pop(stacknode *st)
{
if(st->top>0)  st->top--;
    else  printf("Stack is Empty!\n");
}

int main()
{
    char s[M];
    int i;
    stacknode *sp;
    printf("create a empty stack!\n");
    sp=(stacknode *)malloc(sizeof(stacknode));
    init(sp);
    printf("input a expression:\n");
    gets(s);
    for(i=0;i<strlen(s);i++)
    {
        if(s[i]=='(')
            push(sp,s[i]);
        if(s[i]==')')
            pop(sp);
    }
    if(sp->top==0)
        printf("'('match')'!\n");
    else
        printf("'('not match')'!\n");
    return 0;
}

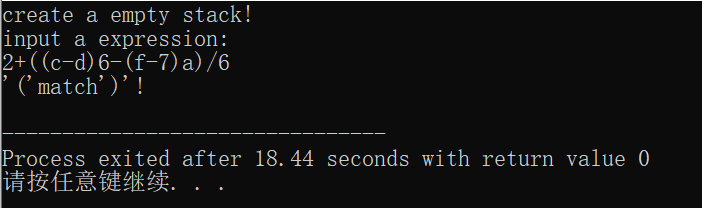
输入：2+((c-d)6-(f-7)a)/6
运行结果：

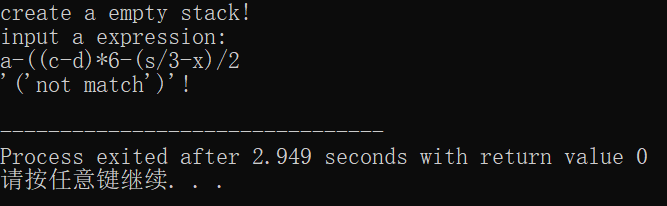
输入：a-((c-d)*6-(s/3-x)/2
运行结果：

程序的基本功能：表达式括号匹配的检验。

四、实验小结
栈和队列的不同思想可用于解决不同的问题需求。栈的先进后出就好比餐盘的洗用，可用于表达式检验括号匹配，进制数转换，中缀表达式转换为后缀表达式求值等等可用先进后出的思想解决的问题。队列的先进先出就好比排队就餐，先来的先取餐，后来的在队尾排队，可用于解决迷宫问题等问题。

posted on 2020-10-21 23:08  lingqing  阅读(130)  评论(0)    收藏  举报

博客园  ©  2004-2026
浙公网安备 33010602011771号 浙ICP备2021040463号-3 Powered By博客园