P11771 题解

blog。虽然是垃圾做法，但是卡了还是半天卡过去了。感谢出题人放宽到 2s /kt！！

---

最显然的暴力是，考虑直接算每个 \(i,j,k\) 的贡献。

• \(p_{i}\le p_k\wedge p_j\le p_k\)：贡献为 \(0\)。
• \(p_{i}>p_k\wedge p_j\le p_k\)：贡献为 \(\min(a,c)\times(p_i-p_k)\)。
• \(p_{i}\le p_k\wedge p_j>p_k\)：贡献为 \(\min(b,c)\times(p_j-p_k)\)。
• \(p_i>p_k\wedge p_j>p_k\)：再分类 \(i,j\) 大小，不妨设 \(p_i<p_j\)，那么贡献为 \(\min(c(p_j-p_k),b(p_j-p_i)+c(p_i-p_k),a(p_i-p_k)+b(p_j-p_k))\)。

注意最后一种情况很难处理，因为要对 \(p\) 做比较，不利于上数据结构。考虑强行化简，记 \(u=p_j-p_k\)，\(v=p_j-p_i\)，那么 \(p_i-p_k=u-v\)，注意这里 \(u\ge0,v\ge0,u-v\ge0\)。上面式子可以写成

\[\min(cu,cu+(b-c)v,(a+b)u-av) \]

分讨一下：

• \(b\le c\) 时等价于 \(\min(cu+(b-c)v,(a+b)u-av)\)，考虑 \(\text{LH}\le\text{RH}\) 等价于 \((a+b-c)(u-v)\ge0\)，而总是有 \(u\ge v\)，因此取左当且仅当 \(a+b\ge c\)，否则取右。
• \(b>c\) 时等价于 \(\min(cu,(a+b)u-av)\)，\(\text{LF}\le\text{RH}\) 等价于 \(a(u-v)+(b-c)u>0\)，总是有 \(u\ge v\) 且 \(b>c\)，因此这个式子是恒成立的，这一部分总是取左即可。

那么现在分析了一大堆，只用在一开始比较下 \(a,b,c\)，剩下的是在二维偏序下求 \(p_i,p_j,p_k\) 相关信息的数据结构题。

---

直接分治是个 BIT 的 2log，但是奈何分讨有点多，感觉不是很能过。

那就考虑直接扫。举例来说，对于 \(p_i>p_k\wedge p_j\le p_k\) 的情况，离散化，从右往左扫 \(i\)，将后面 \(p_j\le p_k\) 的贡献挂在 \(k\) 上维护，那么要查询 \([1,p_i)\) 的贡献，然后再加入 \(i\) 的贡献。具体来说，我们可能会出现三类贡献：\(p_i\) 的、\(p_j\) 的、\(p_k\) 的（例子的这个 case 只有 \(p_j\) 与 \(p_k\) 的贡献）。

• 对于 \(p_i\) 贡献，只用数数，每个点维护 \(F_k\) 表示合法的 \(j\) 的数量（注意这里 \(j,k\) 是值域）。新加入一个 \(j\) 时，\(F_k\) 加上 \(k\) 值域的 \(a\) 数量，记这个值为 \(cnt\)，那就是 \(\forall j\le k\le V,F_k\gets F_k+cnt_k\)，然后 \(cnt_j\gets cnt_j+1\)。
• 对于 \(p_j\) 类似，每次 \(F_k\gets F_k+cnt_k\times j\) 即可。
• 对于 \(p_k\) 类似，每次 \(F_k\gets F_k+tot_k\) 即可，改成维护 \(tot_j\gets tot_j+j\)。

具体转移可以参考下图：

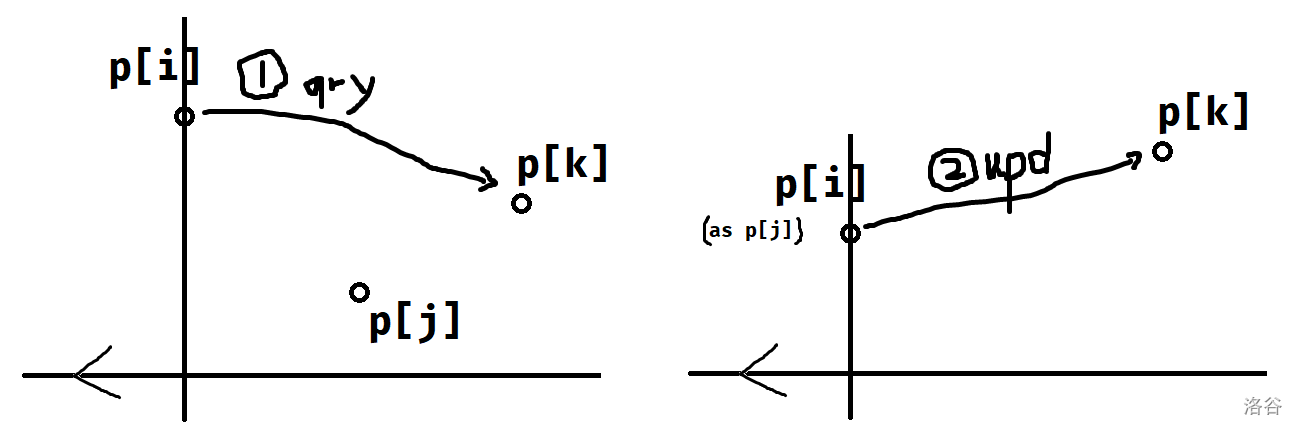
注意操作都是历史和直接加的形式，可以线段树直接维护。另外几种情况都可以相同处理，\(O(n\log n)\)。

但是直接写的话常数太大了，所以要卡常！肯定不能写 \(3\times3\) 矩阵，只用变量做转移；将分讨拆成一棵线段树，常数更小；线段树写 zkw。然后就差不多可以擦时限过了。我跑得实在有点慢，用这个做法跑的比较快的教教我，万分感谢 /bx。

代码一坨史。