一些虚树练习

P4103
看到\(\sum k \leq n\)直接想到建虚树\(dp\)
\(mi_i = min \lbrace dep_v - dep_i \rbrace\)
\(mx_i = max \lbrace dep_v-dep_i\rbrace\)
\(sum_i = \sum dep_v-dep_i\)
\(siz_i\)表示\(i\)的子树内关键点的数量
先处理\(ans_{max}，ans_{min}\)
可以发现，两个关键点之间的距离会跨越根节点.

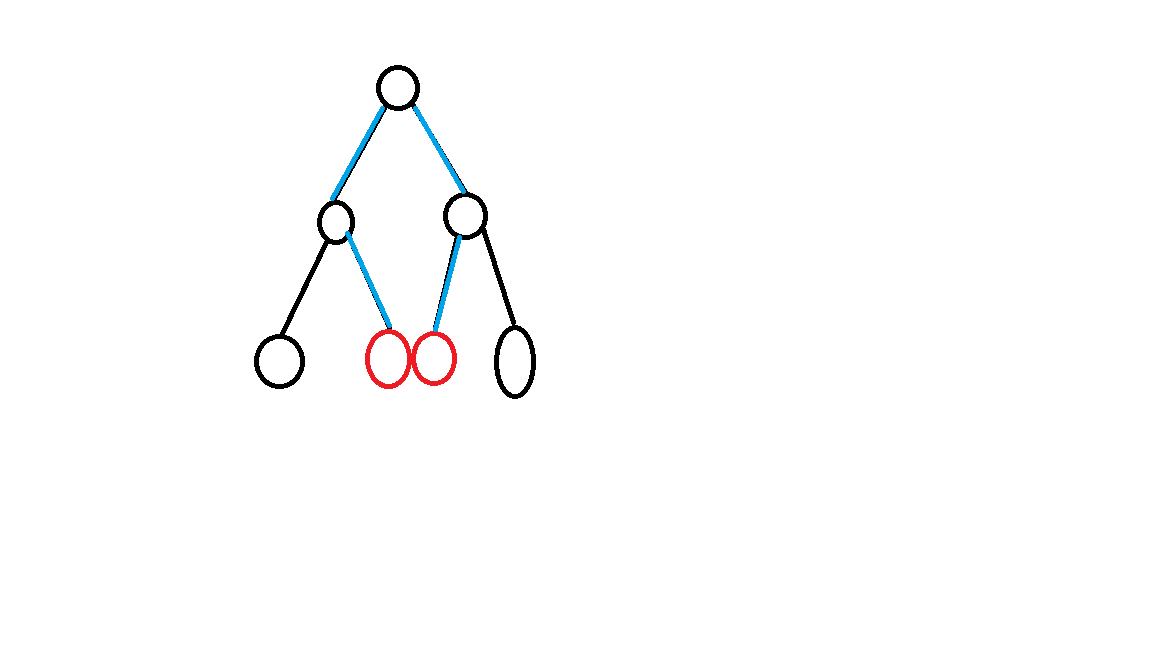
蓝色的就是这一条边的长度，不妨拆成两部分。

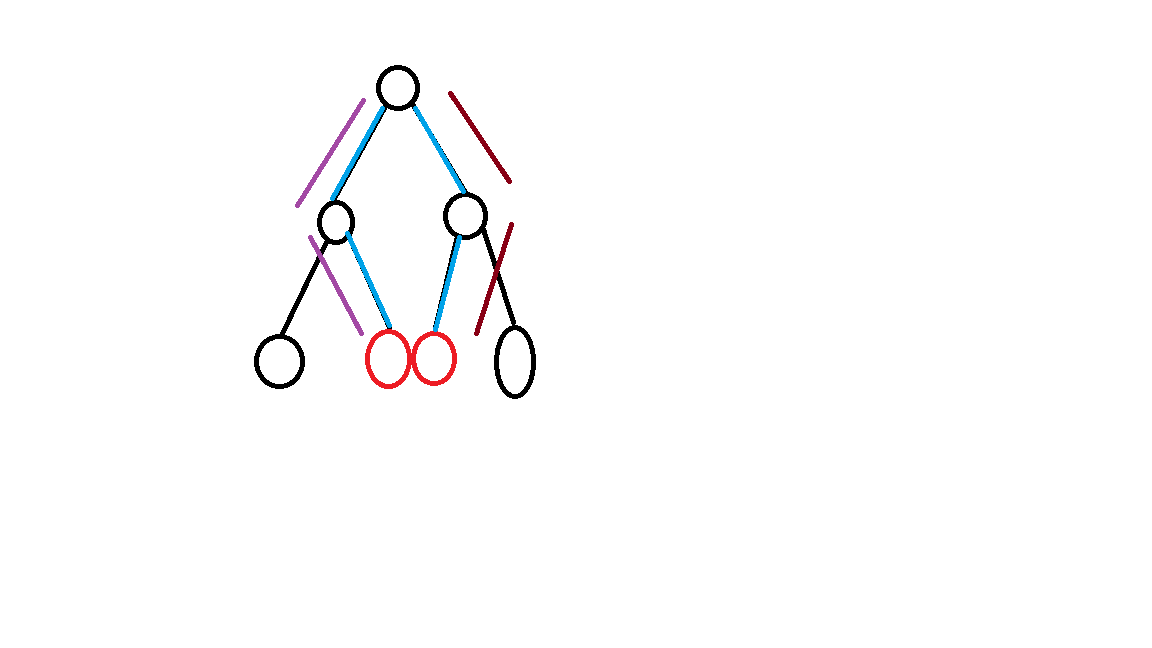
紫色与棕色的两部分可以在分别的子树中处理出来，考虑如何合并子树的信息。
假设现在枚举到的子节点编号为\(v_i\),则在遍历这个子节点前我们处理了\(v_1 \dots v_{i-1}\)合并后的信息。
记最终答案分别为\(ans_{max},ans_{min},ans_{sum}\)，\(dep_{v_i}-dep_u=l\)
那么前\(i-1\)个子节点都可以与第\(i\)个子节点的信息进行合并。以处理\(ans_{min}\)为例。
目前我们已知根据前\(i-1\)个子节点的\(ans_{min}\)与根据前\(i-1\)个子节点合并得出的\(mi_u\)
则前\(i-1\)个子节点与第\(i\)个子节点合并得出的有效信息即为：\(mi_u + l + mi_{v_i}\)
展开说明：我们现在计算的是前\(i-1\)个子节点子树中的一条边与第\(i\)个子节点子树中的一条边连成的边的最小值。
所以我们使前\(i-1\)个子节点的信息最小且使第\(i\)个子节点的信息最小即得整体最小。
最后在更新一下$mi_u = min \lbrace mi_{v_i}+l \rbrace $。

计算\(ans_{max} , mx_{u}\)同理，最后处理棘手的\(ans_{sum},sum_u\)
如上，假设现在已经处理合并好了前\(i-1\)个子节点的信息。
可以知道我们要计算的是前\(i-1\)个子节点的信息总和与\(v_i\)信息总和的合并。
暴力的想，其实就是把前\(i-1\)个子节点的子树中的所有边与\(v_i\)子树中的边一条条匹配求和。
我们有\(sum_u\)表示根据前\(i-1\)个子节点计算出的每个子树内边的长度和，与\(v_i\)的长度和\(sum_{v_i}\)
直接拿出来匹配即可：\(sum_u\times siz_v + l \times siz_u \times siz_v + sum_v \times siz_u\)
展开说明：乘法原理得\(v_i \rightarrow u\)被走了\(siz_u \times siz_v\)次，\(v_1 \dots v_{i-1}\)与\(v_i\)内的边互相匹配。
最后更新\(sum_u \leftarrow sum_u+sum_v+l\times siz_v\)

时间复杂度\(O(qklogk)\approx O(nlogn)\)

---

P3233
考虑朴素做法，一个点对应的议事点不是在它的子树内就是在子树外。可以通过两遍\(dfs\)求出对应的议事点。
我们考虑建棵虚树，在虚树上的点可以通过朴素算法求出，不在虚树上的点分两种情况。
\((i)\)在原树上的节点\(u\)，如果它有一个子树根节点为\(v\)，且这个子树内没有议事点，则整棵子树的点都会贡献到\(u\)的议事点上。
\((ii)\)在虚树上的一条边\(u\rightarrow v\)，对应着原树上的一条链。这条链上的节点一定是分成两部分（可以为空）分别贡献到\(u\)的议事点和\(v\)的议事点上的，考虑倍增找到这个分界点。
具体实现：
\((i)\)对于虚树上的一条边\(u\rightarrow v\)，我们找到原树上这条链中\(u\)的子节点\(w\)，则以\(w\)为根的子树中含有议事点，无法根据情况一贡献，减去\(siz_w\)即可。对于总贡献，用\(siz_u-\sum siz_w\)即可。
\((ii)\)我们可以预处理原树上的深度，在\(u\rightarrow v\)这条链上倍增，类似与\(LCA\)往上倍增到分界点即可。
最后\(u,v\)分别加上对应的贡献。
时间复杂度\(O(qmlogm)\approx O(nlogn)\)