一下午讲了 9 道题？！

省选模拟

CQXYM的线性规划

考虑到 \(x \in \{0,1\}\)，显然并不能套用线性规划的做法。

观察到 \(a_i \leq b_i\)，那么原限制相当于是对于所有 \(x_i=1\) 的物品，在 \([a_i,b_i]\) 区间内选一个数进行贡献，要求最后的贡献和 \(=p\)。

直接设 \(f_{i,j}\) 表示决策了前 \(i\) 个物品，当前总贡献为 \(j\)，转移讨论当前物品选还是不选，以及具体的权值。

\[f_{i,j}=\max(f_{i-1,j},\max_{k=j-b_i}^{j-a_i} f_{i-1,k}+c_i) \]

显然可以使用单调队列进行优化，总复杂度 \(O(nV)\)。

路径染色

• 考虑先把所有决策都设为 \(A\)，再将其中一部分转化为 \(B\)。

观察数据范围和贡献形式不难猜出需要用费用流。

考虑先假设所有的路径都染成蓝色，然后把其中一部分转换成红色。

对于每条边原本至多有 \(r\) 条红色路径和 \(b\) 条蓝色路径的限制就转化为了形如每条边的红色路径条数必须处于区间 \([l,r]\) 内的限制。

考虑分别连边表示每条路径改变颜色还是不变，并利用树边处理区间限制，如下图：

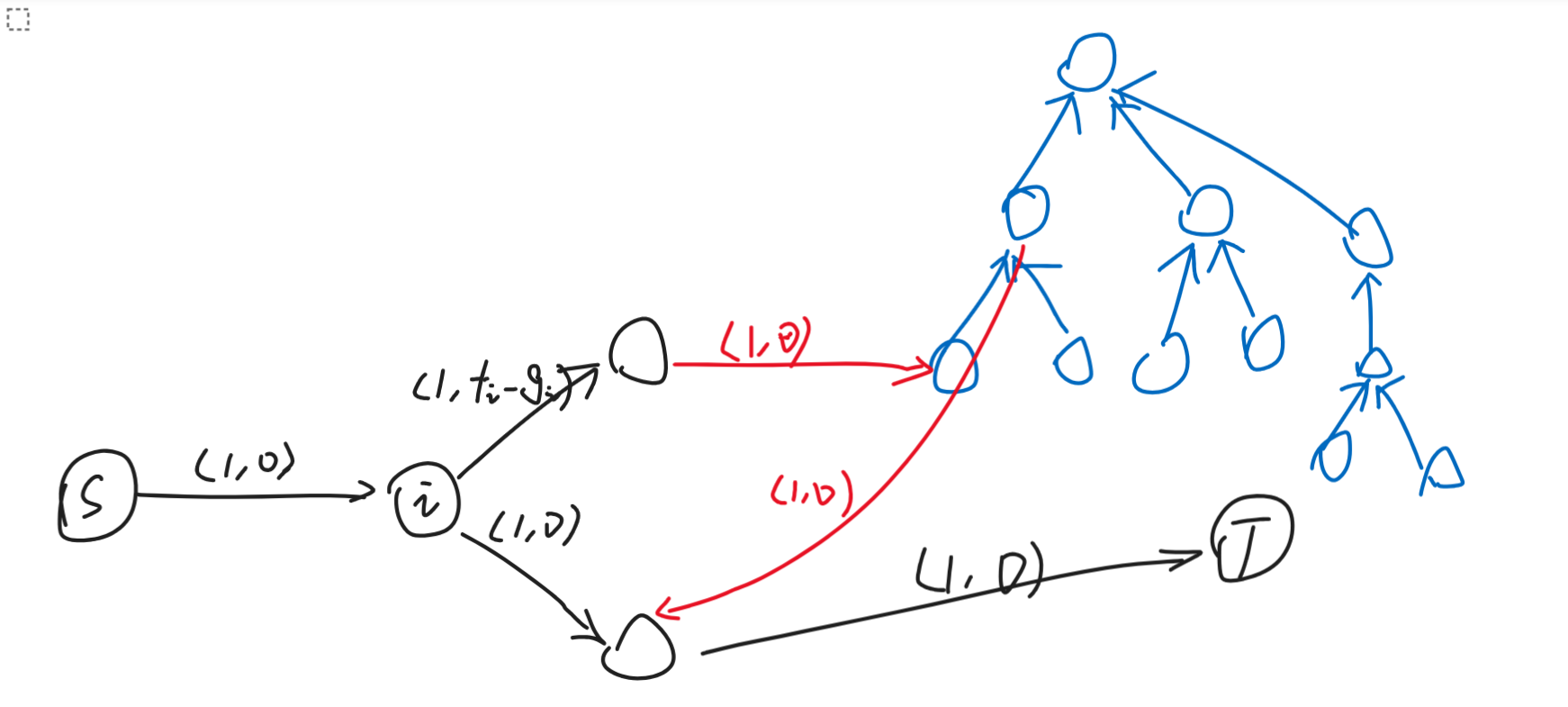
其中 \(f_i\) 和 \(g_i\) 分别表示第 \(i\) 条路径选红色和蓝色所造成的总贡献。

建出图后直接跑有源汇上下界最小费用最大流即可，但是注意到这样子建图在添加额外边后可能会产生负权回路。

当然可以使用一些手法去掉负权边，但是可以考虑另一种建图，不提前假定所有的路径都染成蓝色，而是用两条边分别表示染成红色和蓝色：

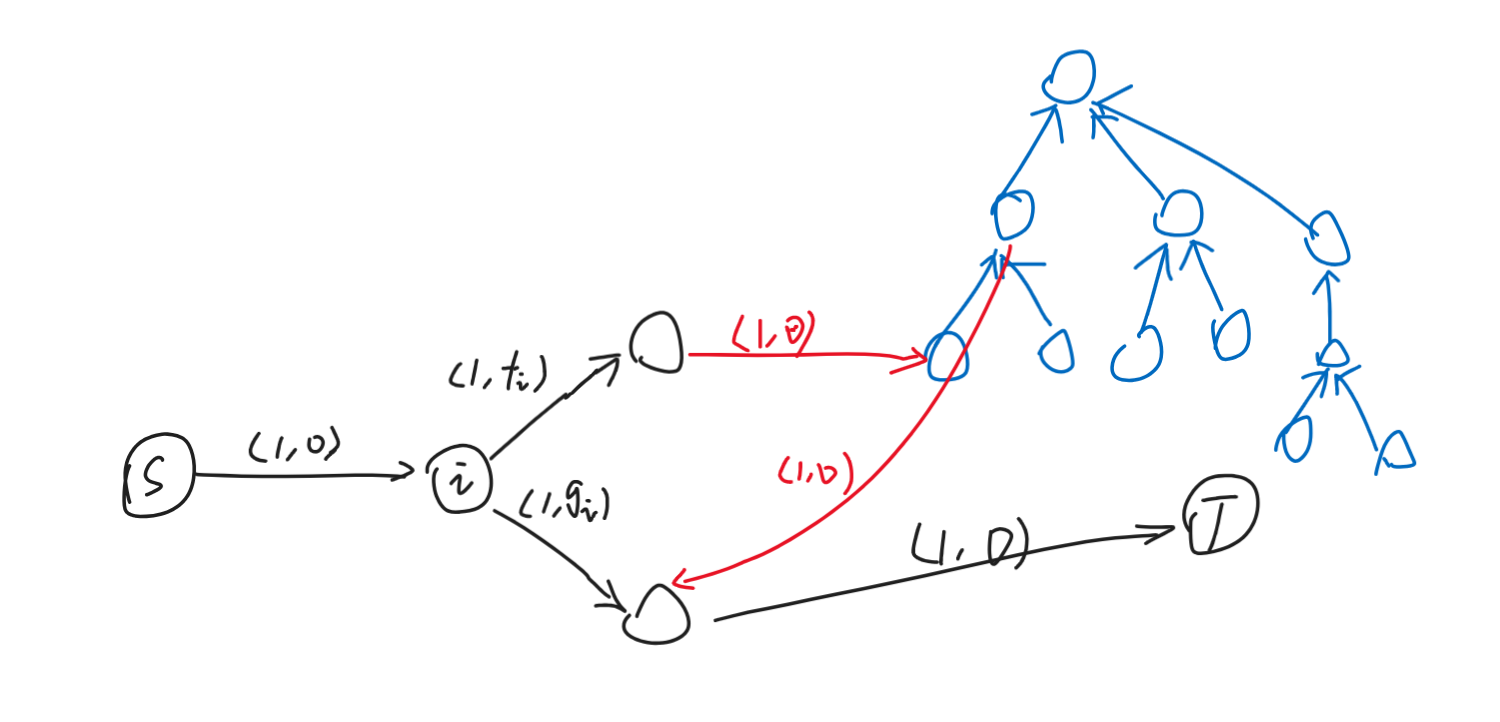
非常优雅。

\(\text{The 4th Universal Cup. Stage 13: Grand Prix of Ōokayama}\)

\(\text{Depth of Interval}\)

• 在一个排列 \(p\) 中，令 \(S_k(l,r)\) 表示由第 \(l\) 个到第 \(r\) 个所有元素中的前 \(k\) 大的元素的下标所组成的集合，若 \(r-l+1 \leq k\)，\(S_k(l,r)\) 则为区间内所有下标组成的集合，设 \(M=\{S_k(l,r)|1 \leq l \leq r \leq n\}\)，有 \(O(|M|)=O(nk)\)，即所有子区间的前 \(k\) 大集合中本质不同的集合仅有 \(O(nk)\) 个。

考虑从左到右加入数，假设当前已经考虑到了第 \(i\) 个数。

我们钦定当前的一个后缀 \([j,i]\) 是关键的，当且仅当 \(j=i\) 或者 \(S_k(j,i) \not= S_k(j+1,i)\)。

显然，\([j,i]\) 为关键后缀的充要条件是 \([j+1,i]\) 内 \(> p_j\) 的数的个数 \(< k\) 个。这是因为如果这样的数的个数 \(\ge k\) 个，\(p_j\) 就不可能被包含在前 \(k\) 大区间中，故 \(S_k(j,i)=S_k(j+1,i)\)。

\(|M|\) 即为加入数的整个过程中，关键后缀的总数量。

考虑用链表记录下所有的 \(j\)，满足 \([j,i]\) 为关键后缀，对于链表中的每一个元素，赋予其初始势能为 \(k-x\)，其中 \(x\) 为 \([j+1,i]\) 中 \(>p_j\) 的数的个数，接下来进行加入一个数 \(v\) 的操作。

沿链表从右往左跳，并同时记录目前比 \(v\) 大的关键后缀左端点个数 \(cnt\)，若 \(v>p_j\) 则将 \(j\) 的势能减少 \(1\)，否则将 \(cnt\) 增加 \(1\)。

当一个关键后缀的势能减为 \(0\) 时，它就不再关键，直接从链表中删去即可。

当 \(cnt\) 减为 \(0\) 时，就不会再对更靠左的关键区间造成影响，直接退出这个过程。

根据初始势能，容易分析出这个过程的总复杂度是 \(O(nk)\) 的，故上述结论得证。