有序表专题笔记
有序表的定义:
可以完成查询操作,key有对应的value,且表中是有序的。做到这个的复杂度为O(logn),例如map
注意:比赛中一般用静态结构省时间。在工程中一般用动态结构,防止内存泄漏
实现的数据结构
·AVL
1.结构定义:|左树高度-右树高度|<=1(平衡二叉树)
2.基本操作:左旋和右旋
3.四种违规情况
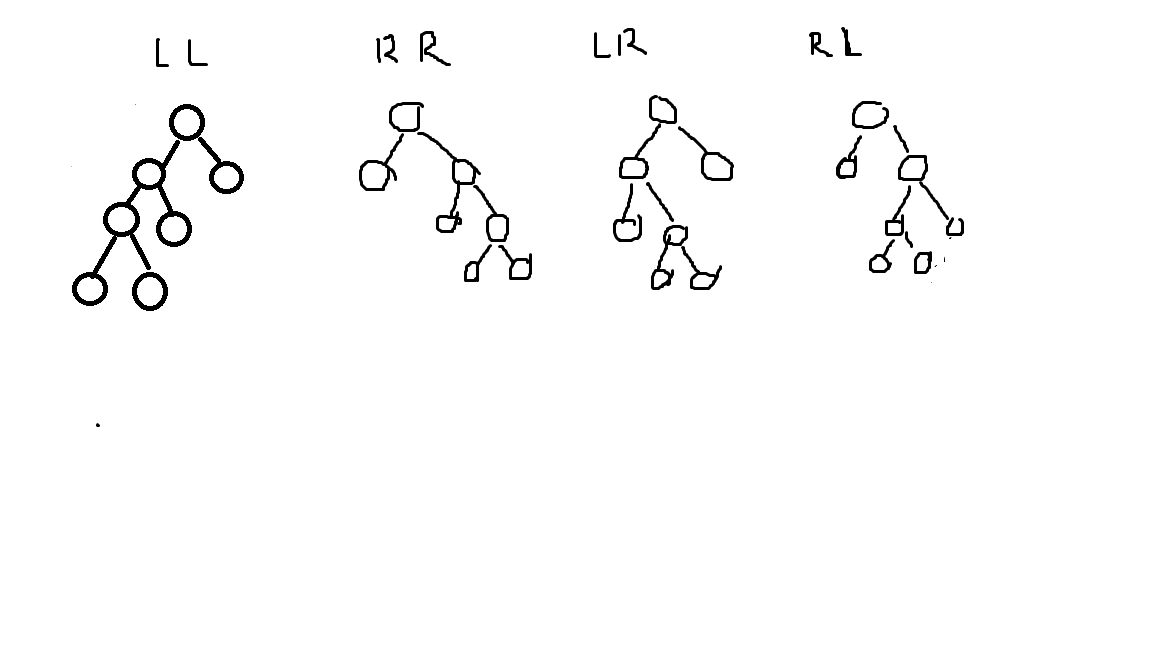
1)LL 左树高度-右树高度>1 ,且左节点的左树高度>=右树高度 解决方案:右旋
2)RR 右树高度-左树高度>1 ,且右节点的右树高度>=左树高度 解决方案:左旋
3)LR 左树高度-右树高度>1 ,且左节点的左树高度<右树高度 解决方案:左树左旋,整棵树右旋
4)RL 右树高度-左树高度>1 ,且右节点的右树高度<左树高度 解决方案:右树右旋,整棵树左旋
https://leetcode.cn/problems/queue-reconstruction-by-height/description/
https://www.luogu.com.cn/problem/P3369
基本操作代码(即洛谷P3369)如下
#include<bits/stdc++.h>
using namespace std;
const int maxn=100001;
int key[maxn],_left[maxn],_right[maxn],sizes[maxn],_count[maxn],height[maxn],cnt;
int head;
void up(int i)//整合
{
sizes[i]=sizes[_left[i]]+sizes[_right[i]]+_count[i];
height[i]=max(height[_left[i]],height[_right[i]])+1;
}
int zag(int i)//左旋
{
int r=_right[i];
_right[i]=_left[r];
_left[r]=i;
up(i);
up(r);
return r;
}
int zig(int i)//右旋
{
int l=_left[i];
_left[i]=_right[l];
_right[l]=i;
up(i);
up(l);
return l;
}
int maintain(int i)//平衡
{
int lh=height[_left[i]],rh=height[_right[i]];
if(lh-rh>1)
{
if(height[_left[_left[i]]]>=height[_right[_left[i]]])//LL
{
i=zig(i);
}
else//LR
{
_left[i]=zag(_left[i]);
i=zig(i);
}
}
else if(rh-lh>1)
{
if(height[_right[_right[i]]]>=height[_left[_right[i]]])
{
i=zag(i);
}
else
{
_right[i]=zig(_right[i]);
i=zag(i);
}
}
return i;//这里不需要up整合,因为zig和zag已经整合了
}
int add(int i,int x)
{
if(i==0)
{
key[++cnt]=x;
height[cnt]=sizes[cnt]=_count[cnt]=1;
return cnt;
}
if(key[i]==x)
{
_count[i]++;
}
else if(key[i]>x)
{
_left[i]=add(_left[i],x);
}
else
{
_right[i]=add(_right[i],x);
}
up(i);
return maintain(i);
}
int small(int i,int v)//计算比自己小的数有多少
{
if(i==0)
return 0;
if(key[i]>=v)
{
return small(_left[i],v);
}
else
{
return small(_right[i],v)+sizes[_left[i]]+_count[i];
}
}
int _rank(int v)//计算自己的排位
{
return small(head,v)+1;
}
int removemostleft(int i,int mostleft)//因为要往上调整,所以要用递归调用
{
if(i==mostleft)
return _right[i];
else
{
_left[i]=removemostleft(_left[i],mostleft);
up(i);
return maintain(i);
}
}
int remove(int i,int v)
{
if(key[i]<v)
_right[i]=remove(_right[i],v);
else if(key[i]>v)
_left[i]=remove(_left[i],v);
else
{
if(_count[i]>1)
_count[i]--;
else
{
if(_left[i]==_right[i])
return 0;
else if(_left[i]!=0 && _right[i]==0)
{
i=_left[i];
}
else if(_right[i]!=0 && _left[i]==0)
{
i=_right[i];
}
else
{
int mostleft=_right[i];
while(_left[mostleft]!=0)
mostleft=_left[mostleft];
_right[i]=removemostleft(_right[i],mostleft);
_left[mostleft]=_left[i];
_right[mostleft]=_right[i];
i=mostleft;
}
}
}
up(i);
return maintain(i);
}
void checkremove(int v)
{
if(_rank(v)!=_rank(v+1))//有v这个数
{
head=remove(head,v);
}
}
int index(int i,int x)//排在第x的数是啥
{
if(sizes[_left[i]]>=x)
return index(_left[i],x);
else if(sizes[_left[i]]+_count[i]<x)
return index(_right[i],x-sizes[_left[i]]-_count[i]);
return key[i];
}
int findindex(int x)
{
return index(head,x);
}
int pre(int i,int x)
{
if(i==0)
return INT_MIN;
if(key[i]>=x)
return pre(_left[i],x);
else
{
return max(key[i],pre(_right[i],x));
}
}
int findpre(int x)//前驱
{
return pre(head,x);
}
int post(int i,int x)
{
if(i==0)
return INT_MAX;
if(key[i]<=x)
return post(_right[i],x);
else
{
return min(key[i],post(_left[i],x));
}
}
int findpost(int x)//后驱
{
return post(head,x);
}
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int op,x;
cin>>op>>x;
if(op==1)
{
head=add(head,x);
}
else if(op==2)
{
checkremove(x);
}
else if(op==3)
{
cout<<_rank(x)<<"\n";
}
else if(op==4)
{
cout<<findindex(x)<<"\n";
}
else if(op==5)
{
cout<<findpre(x)<<"\n";
}
else
{
cout<<findpost(x)<<"\n";
}
}
return 0;
}
·替罪羊树
α一般取0.7
注意:这里是double类型,我原来写成了int调了好久QAQ
具体代码如下
#include<bits/stdc++.h>
using namespace std;
const int maxn=100001;
const double alpha=0.7;
int ci,top,fa,lor;
int key[maxn],collect[maxn],_left[maxn],_right[maxn],sizes[maxn],_count[maxn],diff[maxn],cnt;
int head;
int init(int num)//新建节点
{
key[++cnt]=num;
_count[cnt]=sizes[cnt]=diff[cnt]=1;
return cnt;
}
void up(int i)
{
sizes[i]=sizes[_left[i]]+sizes[_right[i]]+_count[i];
diff[i]=diff[_left[i]]+diff[_right[i]]+(_count[i]>0?1:0);
}
void inorder(int i)//中序遍历收集节点
{
if(i!=0)
{
inorder(_left[i]);
if(_count[i]>0)
collect[++ci]=i;
inorder(_right[i]);
}
}
int build(int l,int r)//二分重置顺序
{
if(l>r)
return 0;
int m=(l+r)>>1;
int h=collect[m];
_left[h]=build(l,m-1);
_right[h]=build(m+1,r);
up(h);
return h;
}
void rebuild()
{
if(top!=0)//有不平衡,top为最上方不平衡节点
{
ci=0;
inorder(top);
if(ci>0)
{
if(fa==0)//整棵树的头结点是需要平衡调节
head=build(1,ci);
else if(lor==1)
_left[fa]=build(1,ci);
else
_right[fa]=build(1,ci);
}
}
}
bool balance(int i)
{
return alpha*diff[i]>=max(diff[_left[i]],diff[_right[i]]);
}
void add(int i,int f,int s,int num)
{
if(i==0)
{
if(f==0)
head=init(num);
else if(s==1)
_left[f]=init(num);
else
_right[f]=init(num);
}
else
{
if(key[i]==num)
_count[i]++;
else if(key[i]>num)
add(_left[i],i,1,num);
else
add(_right[i],i,2,num);
}
up(i);
if(!balance(i))
{
top=i;
fa=f;
lor=s;
}
}
void prepareadd(int num)
{
top=fa=lor=0;
add(head,0,0,num);
rebuild();
}
int small(int i,int num)
{
if(i==0) return 0;
if(key[i]>=num)
return small(_left[i],num);
else
return sizes[_left[i]]+_count[i]+small(_right[i],num);
}
int _rank(int num)
{
return small(head,num)+1;
}
int index(int i,int x)
{
if(sizes[_left[i]]>=x)
return index(_left[i],x);
else if(sizes[_left[i]]+_count[i]<x)
return index(_right[i],x-sizes[_left[i]]-_count[i]);
return key[i];
}
int findindex(int x)
{
return index(head,x);
}
int pre(int num)
{
int kth=_rank(num);
if(kth==1)
return INT_MIN;
else
return findindex(kth-1);
}
int post(int num)
{
int kth=_rank(num+1);
if(kth==sizes[head]+1)
return INT_MAX;
else
return findindex(kth);
}
void remove(int i,int f,int s,int num)
{
if(key[i]==num)
_count[i]--;
else if(key[i]>num)
remove(_left[i],i,1,num);
else
remove(_right[i],i,2,num);
up(i);
if(!balance(i))
{
top=i;
fa=f;
lor=s;
}
}
void checkremove(int num)
{
if(_rank(num)!=_rank(num+1))
{
top=fa=lor=0;
remove(head,0,0,num);
rebuild();
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin>>n;
for(int i=0;i<n;i++)
{
int op,x;
cin>>op>>x;
if(op==1)
{
prepareadd(x);
}
else if(op==2)
{
checkremove(x);
}
else if(op==3)
{
cout<<_rank(x)<<"\n";
}
else if(op==4)
{
cout<<findindex(x)<<"\n";
}
else if(op==5)
{
cout<<pre(x)<<"\n";
}
else
{
cout<<post(x)<<"\n";
}
}
return 0;
}
咳咳,要不要仔细校准一下,容易眼花QAQ,作者:江海一归客,原文链接:https://chuna2.787528.xyz/jhygk/p/19216715



 浙公网安备 33010602011771号
浙公网安备 33010602011771号