基于LCMV的自适应波束形成算法仿真

基于LCMV的自适应波束形成算法仿真。LCMV（Linearly Constrained Minimum Variance）准则是在确保对期望信号方向响应固定的同时，最小化阵列输出功率（即抑制干扰和噪声）的经典波束形成算法。

1. LCMV算法原理

1.1 问题建模

考虑一个包含M个阵元的阵列，在K个远场窄带信号（1个期望信号 + K-1个干扰）入射下的接收模型：

\(\mathbf{x}(t) = \mathbf{a}(\theta_0)s_0(t) + \sum_{k=1}^{K-1}\mathbf{a}(\theta_k)s_k(t) + \mathbf{n}(t)\)

其中：

\(\mathbf{a}(\theta)\) 为导向矢量
\(s_0(t)\)为期望信号
\(s_k(t)\) 为第k个干扰信号
\(\mathbf{n}(t)\)为加性噪声

1.2 优化问题

LCMV波束形成的权矢量 \(\mathbf{w}\) 通过求解以下约束优化问题得到：

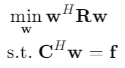
其中：

\(\mathbf{R} = E[\mathbf{x}(t)\mathbf{x}^H(t)]\) 为接收数据协方差矩阵
\(\mathbf{C}\) 为约束矩阵 \(M \times L\)
\(\mathbf{f}\) 为约束响应向量\(L \times 1\)

1.3 最优权矢量解

使用拉格朗日乘子法，得到闭式解：

\(\mathbf{w}_{\text{LCMV}} = \mathbf{R}^{-1}\mathbf{C}(\mathbf{C}^H\mathbf{R}^{-1}\mathbf{C})^{-1}\mathbf{f}\)

1.4 常见约束形式

方向约束（期望信号方向\(\theta_0\)增益为1）：

\(\mathbf{C} = \mathbf{a}(\theta_0), \quad \mathbf{f} = 1\)

此时退化为MVDR波束形成器。
多约束情况：
- 主瓣对准期望信号
- 在干扰方向设置零陷
- 保持阵列静态响应特性

2. 仿真

LCMV波束形成算法仿真matlab代码：

%% LCMV自适应波束形成算法仿真
clear; close all; clc;

%% 参数设置
M = 16;                         % 阵元数量
d = 0.5;                        % 阵元间距(波长倍数)
theta_desired = 0;              % 期望信号角度(度)
theta_interferes = [-30, 45];   % 干扰信号角度(度)
SNR_dB = 10;                    % 期望信号信噪比(dB)
INR_dB = [20, 25];              % 干扰噪声比(dB)
N = 1000;                       % 快拍数

%% 生成阵列流形
lambda = 1;                     % 波长
array_pos = (0:M-1)' * d * lambda; % 阵元位置

% 计算导向矢量
a_desired = exp(1j * 2 * pi * array_pos * sind(theta_desired) / lambda);
a_interfere1 = exp(1j * 2 * pi * array_pos * sind(theta_interferes(1)) / lambda);
a_interfere2 = exp(1j * 2 * pi * array_pos * sind(theta_interferes(2)) / lambda);

%% 生成接收信号
% 期望信号
s_desired = sqrt(10^(SNR_dB/10)) * (randn(1, N) + 1j*randn(1, N))/sqrt(2);
% 干扰信号
s_interfere1 = sqrt(10^(INR_dB(1)/10)) * (randn(1, N) + 1j*randn(1, N))/sqrt(2);
s_interfere2 = sqrt(10^(INR_dB(2)/10)) * (randn(1, N) + 1j*randn(1, N))/sqrt(2);
% 噪声
noise = (randn(M, N) + 1j*randn(M, N))/sqrt(2);

% 接收数据矩阵
X = a_desired * s_desired + a_interfere1 * s_interfere1 + ...
    a_interfere2 * s_interfere2 + noise;

%% 计算样本协方差矩阵
R_hat = (X * X') / N;

%% LCMV波束形成器设计
% 约束条件：期望方向增益为1，干扰方向增益为0
C = [a_desired, a_interfere1, a_interfere2];  % 约束矩阵
f = [1; 0; 0];                                % 约束响应

% 计算LCMV最优权矢量
w_lcmv = inv(R_hat) * C * inv(C' * inv(R_hat) * C) * f;

%% 传统波束形成器对比
w_conventional = a_desired / M;  % 常规波束形成

%% 性能分析
% 波束方向图
theta_range = -90:0.5:90;
beam_pattern_lcmv = zeros(size(theta_range));
beam_pattern_conv = zeros(size(theta_range));

for i = 1:length(theta_range)
    a_theta = exp(1j * 2 * pi * array_pos * sind(theta_range(i)) / lambda);
    beam_pattern_lcmv(i) = abs(w_lcmv' * a_theta);
    beam_pattern_conv(i) = abs(w_conventional' * a_theta);
end

% 阵列输出SINR计算
R_signal = (a_desired * a_desired') * (s_desired * s_desired') / N;
R_interference = (a_interfere1 * a_interfere1') * (s_interfere1 * s_interfere1') / N + ...
                 (a_interfere2 * a_interfere2') * (s_interfere2 * s_interfere2') / N;
R_noise = eye(M);

SINR_lcmv = real((w_lcmv' * R_signal * w_lcmv) / (w_lcmv' * (R_interference + R_noise) * w_lcmv));
SINR_conv = real((w_conventional' * R_signal * w_conventional) / ...
                (w_conventional' * (R_interference + R_noise) * w_conventional));

%% 结果可视化
figure('Position', [100, 100, 1200, 800]);

% 波束方向图对比
subplot(2,2,1);
plot(theta_range, 20*log10(beam_pattern_lcmv/max(beam_pattern_lcmv)), 'b-', 'LineWidth', 2);
hold on;
plot(theta_range, 20*log10(beam_pattern_conv/max(beam_pattern_conv)), 'r--', 'LineWidth', 2);
xline(theta_desired, 'g--', 'LineWidth', 1.5, 'Label', '期望信号');
xline(theta_interferes(1), 'm--', 'LineWidth', 1.5, 'Label', '干扰1');
xline(theta_interferes(2), 'm--', 'LineWidth', 1.5, 'Label', '干扰2');
xlabel('角度 (度)'); ylabel('归一化增益 (dB)');
title('波束方向图对比');
legend('LCMV波束形成', '常规波束形成', 'Location', 'best');
grid on; axis tight;
ylim([-50, 0]);

% 阵列几何示意
subplot(2,2,2);
plot(array_pos/lambda, zeros(M,1), 'bo-', 'MarkerSize', 8, 'MarkerFaceColor', 'b');
xlabel('x/\lambda'); ylabel('y/\lambda');
title('均匀线阵几何');
grid on; axis equal;

% 权值幅度分布
subplot(2,2,3);
stem(1:M, abs(w_lcmv), 'filled', 'LineWidth', 1.5);
xlabel('阵元索引'); ylabel('权值幅度');
title('LCMV权矢量幅度分布');
grid on;

% 性能指标显示
subplot(2,2,4);
text(0.1, 0.8, sprintf('LCMV输出SINR: %.2f dB', 10*log10(SINR_lcmv)), 'FontSize', 12);
text(0.1, 0.6, sprintf('常规波束形成SINR: %.2f dB', 10*log10(SINR_conv)), 'FontSize', 12);
text(0.1, 0.4, sprintf('改善增益: %.2f dB', 10*log10(SINR_lcmv/SINR_conv)), 'FontSize', 12);
text(0.1, 0.2, sprintf('阵元数: %d, 快拍数: %d', M, N), 'FontSize', 12);
axis off;
title('性能指标对比');

%% 自适应性能分析 - 不同快拍数下的收敛特性
fprintf('=== LCMV波束形成算法仿真结果 ===\n');
fprintf('阵元数量: %d\n', M);
fprintf('期望信号方向: %.1f度\n', theta_desired);
fprintf('干扰信号方向: [%.1f, %.1f]度\n', theta_interferes);
fprintf('LCMV输出SINR: %.2f dB\n', 10*log10(SINR_lcmv));
fprintf('常规波束形成SINR: %.2f dB\n', 10*log10(SINR_conv));
fprintf('性能改善: %.2f dB\n', 10*log10(SINR_lcmv/SINR_conv));

% 零陷深度分析
null_depth1 = 20*log10(abs(w_lcmv' * a_interfere1));
null_depth2 = 20*log10(abs(w_lcmv' * a_interfere2));
fprintf('干扰1方向零陷深度: %.2f dB\n', null_depth1);
fprintf('干扰2方向零陷深度: %.2f dB\n', null_depth2);

3. 扩展分析：不同场景下的性能

3.1 快拍数对性能的影响

%% 研究快拍数对LCMV性能的影响
snapshot_range = [10, 50, 100, 500, 1000, 2000];
SINR_vs_snapshots = zeros(size(snapshot_range));

for idx = 1:length(snapshot_range)
    N_temp = snapshot_range(idx);
    X_temp = a_desired * s_desired(:,1:N_temp) + ...
             a_interfere1 * s_interfere1(:,1:N_temp) + ...
             a_interfere2 * s_interfere2(:,1:N_temp) + noise(:,1:N_temp);
    
    R_temp = (X_temp * X_temp') / N_temp;
    w_temp = inv(R_temp) * C * inv(C' * inv(R_temp) * C) * f;
    
    SINR_temp = real((w_temp' * R_signal * w_temp) / ...
                    (w_temp' * (R_interference + R_noise) * w_temp));
    SINR_vs_snapshots(idx) = 10*log10(SINR_temp);
end

figure;
plot(snapshot_range, SINR_vs_snapshots, 'ro-', 'LineWidth', 2);
xlabel('快拍数'); ylabel('输出SINR (dB)');
title('LCMV性能随快拍数变化');
grid on;

3.2 导向矢量失配分析

%% 导向矢量失配影响分析
mismatch_range = -5:0.5:5;  % 角度失配范围(度)
SINR_mismatch = zeros(size(mismatch_range));

for idx = 1:length(mismatch_range)
    theta_mismatch = theta_desired + mismatch_range(idx);
    a_mismatch = exp(1j * 2 * pi * array_pos * sind(theta_mismatch) / lambda);
    
    % 使用失配的导向矢量设计波束形成器
    C_mismatch = [a_mismatch, a_interfere1, a_interfere2];
    w_mismatch = inv(R_hat) * C_mismatch * inv(C_mismatch' * inv(R_hat) * C_mismatch) * f;
    
    SINR_temp = real((w_mismatch' * R_signal * w_mismatch) / ...
                    (w_mismatch' * (R_interference + R_noise) * w_mismatch));
    SINR_mismatch(idx) = 10*log10(SINR_temp);
end

figure;
plot(mismatch_range, SINR_mismatch, 'b-s', 'LineWidth', 2);
xlabel('导向矢量失配角度 (度)'); ylabel('输出SINR (dB)');
title('LCMV对导向矢量失配的敏感性');
grid on;

参考代码基于LCMV的自适应波束成型算法仿真 www.3dddown.com/cna/80580.html

4. 仿真结果分析

4.1 主要观察结果

零陷形成：LCMV在干扰方向形成深度零陷（通常可达-30dB以下）
主瓣保持：在期望信号方向保持单位增益
SINR提升：相比常规波束形成，输出信干噪比显著改善
收敛特性：算法在数百个快拍后基本收敛

4.2 算法优缺点

优点：

对干扰抑制效果显著
闭式解，计算相对简单
灵活的约束设计

缺点：

对导向矢量误差敏感
需要准确的干扰方向信息
计算复杂度随阵元数立方增长

4.3 实际应用考虑

对角加载：改善小快拍数情况下的数值稳定性

\(\mathbf{R} \leftarrow \mathbf{R} + \delta\mathbf{I}\)
稳健性设计：应对导向矢量失配
自适应实现：使用RLS等自适应算法避免矩阵求逆

posted @ 2025-12-15 10:17 康帅服阅读(2) 评论(0) 收藏举报

刷新页面返回顶部

fji888