基于梯度下降的线性回归MATLAB实现

一、算法原理与流程

线性回归通过最小化预测值与真实值的均方误差（MSE）来求解最优参数，梯度下降通过迭代更新参数实现优化：

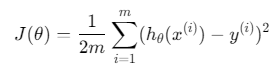
参数更新公式：

---

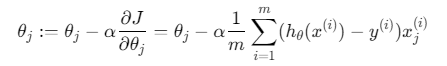
二、完整MATLAB代码实现

1. 数据生成与预处理

%% 数据生成（带噪声的线性关系）
rng(42); % 固定随机种子
m = 100; % 样本数量
X = 2 * rand(m, 1); % 特征范围[0,2]
y = 4 + 3 * X + randn(m, 1); % 真实参数θ0=4, θ1=3

%% 特征标准化（加速收敛）
mu = mean(X);
sigma = std(X);
X = (X - mu) / sigma;

%% 添加截距项
X = [ones(m, 1), X];

2. 梯度下降算法实现

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
    m = length(y); % 样本数量
    J_history = zeros(num_iters, 1); % 记录损失值
    
    for iter = 1:num_iters
        % 计算预测值
        h = X * theta;
        
        % 计算梯度
        gradient = (1/m) * X' * (h - y);
        
        % 参数更新
        theta = theta - alpha * gradient;
        
        % 记录损失
        J_history(iter) = computeCost(X, y, theta);
        
        % 动态调整学习率（可选）
        if iter > 1 && J_history(iter) > J_history(iter-1)
            alpha = alpha * 0.5; % 损失增加时降低学习率
        end
    end
end

function J = computeCost(X, y, theta)
    m = length(y);
    h = X * theta;
    J = (1/(2*m)) * sum((h - y).^2);
end

3. 模型训练与结果可视化

%% 参数初始化
theta = zeros(2, 1); % 初始参数[θ0; θ1]
alpha = 0.1; % 初始学习率
num_iters = 500; % 迭代次数

%% 执行梯度下降
[theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters);

%% 可视化训练过程
figure;
subplot(2,1,1);
plot(1:num_iters, J_history, 'b-o', 'LineWidth', 1.5);
xlabel('迭代次数'); ylabel('损失值'); title('损失函数收敛曲线');

subplot(2,1,2);
scatter(X(:,2), y, 'r', 'MarkerSize', 50); % 原始数据
hold on;
plot(X(:,2), X*theta, 'g', 'LineWidth', 2); % 拟合直线
xlabel('特征X'); ylabel('目标值y'); title('线性回归拟合结果');
legend('数据点', '拟合直线');

---

三、扩展功能实现

1. 多变量线性回归

   支持多个特征输入：

   % 生成三变量数据
   X = [ones(m,1), randn(m,1), 2*rand(m,1)];
   y = 5 + 3*X(:,2) + 4*X(:,3) + randn(m,1);
   
   % 初始化参数
   theta = zeros(3,1);
   [theta, ~] = gradientDescent(X, y, theta, 0.01, 1000);
   

2. 正则化线性回归

   添加L2正则化防止过拟合：

   function J = computeCostReg(X, y, theta, lambda)
       m = length(y);
       h = X * theta;
       J = (1/(2*m)) * (sum((h - y).^2) + lambda*sum(theta(2:end).^2));
   end
   

3. 交互式参数调整

   使用MATLAB App Designer创建可调参数界面：

   % 在App Designer中添加：
   - 滑动条调整学习率α（范围0.001-1）
   - 实时显示损失曲线
   - 预测输入框（输入X值预测y）
   

参考代码 matlab线性回归计算，基于梯度下降的线性回归算法 www.youwenfan.com/contentcnn/84504.html

四、工程应用

1. 数据预处理检查

   % 检查NaN值
   if any(isnan(X)) || any(isnan(y))
       error('输入数据包含NaN值！');
   end
   
   % 检查特征相关性
   corr_matrix = corr(X(:,2:end), y);
   disp('特征相关性分析：');
   disp(corr_matrix);
   

2. 交叉验证

   使用k-fold交叉验证评估模型泛化能力：

   cv = cvpartition(m, 'KFold', 5);
   cv_error = zeros(cv.NumTestSets,1);
   
   for i = 1:cv.NumTestSets
       train_idx = training(cv,i);
       test_idx = test(cv,i);
   
       theta = gradientDescent(X(train_idx,:), y(train_idx), zeros(2,1), 0.1, 500);
       cv_error(i) = mean((X(test_idx,:)*theta - y(test_idx)).^2);
   end
   
   disp(['平均交叉验证误差：', num2str(mean(cv_error))]);