卡尔曼滤波与PID控制的协同:滤波降噪与系统优化
一、核心原理:卡尔曼滤波与PID的互补性
卡尔曼滤波(Kalman Filter)与PID控制的结合,本质上是状态估计与反馈控制的协同优化。其核心逻辑如下:
- 卡尔曼滤波的降噪作用 通过动态系统建模(状态方程和观测方程),卡尔曼滤波对含噪声的传感器数据进行最优状态估计,抑制高斯白噪声干扰。例如,在电机转速控制中,编码器数据可能因机械振动产生高频噪声,卡尔曼滤波可提取平滑的真实转速。
- PID控制的误差修正 PID控制器基于滤波后的状态误差(如位置偏差、速度偏差)生成控制量,避免噪声直接干扰控制决策。例如,在无人机姿态控制中,IMU的陀螺仪噪声经过滤波后,PID可更精准地调整电机推力。
二、实现流程与关键步骤
1. 系统建模与参数设计
-
状态方程:描述系统动态(如位置、速度变化)
\(x_k=Ax_{k−1}+Bu_{k−1}+w_k\)
其中,\(w_k\)为过程噪声(协方差矩阵\(Q\))。
-
观测方程:描述传感器测量模型
\(z_k=Hx_k+v_k\)
其中,\(v_k\)为测量噪声(协方差矩阵\(R\))。
-
PID参数整定:根据系统响应特性调整\(K_p,K_i,K_d\),通常采用Ziegler-Nichols法或试凑法。
2. 卡尔曼滤波降噪实现
% MATLAB示例:卡尔曼滤波对传感器数据降噪
A = 1; % 状态转移矩阵(一阶系统)
H = 1; % 观测矩阵
Q = 0.01; % 过程噪声协方差
R = 0.1; % 测量噪声协方差
% 初始化
x_hat = 0; % 初始状态估计
P = 1; % 初始协方差
% 模拟含噪声测量数据
true_signal = sin(0.1 * 0:0.01:10); % 真实信号
noise = sqrt(R)*randn(size(true_signal));
measured_signal = true_signal + noise;
% 卡尔曼滤波迭代
filtered_signal = zeros(size(measured_signal));
for k = 2:length(measured_signal)
% 预测
x_hat_pred = A * x_hat;
P_pred = A * P * A' + Q;
% 更新
K = P_pred * H' / (H * P_pred * H' + R);
x_hat = x_hat_pred + K * (measured_signal(k) - H * x_hat_pred);
P = (1 - K * H) * P_pred;
filtered_signal(k) = x_hat;
end
3. PID控制与滤波数据融合
-
输入处理:将卡尔曼滤波输出作为PID的反馈信号。
-
控制量计算:
![]()
其中,\(e(k)=r(k)−x_{hat}(k)\)为滤波后的误差。
-
抗积分饱和:对积分项限幅,避免长时间误差累积。
三、性能优化
1. 卡尔曼滤波参数自适应
- 噪声协方差在线调整:根据系统状态变化动态更新Q和R(如基于新息协方差分析)。
- 多模型融合:针对非线性系统,采用扩展卡尔曼滤波(EKF)或无迹卡尔曼滤波(UKF)。
2. PID参数自整定
- 基于滤波信号的频域分析:通过FFT分析滤波后信号的频谱,优化PID参数以抑制特定频率噪声。
- 鲁棒性增强:引入前馈补偿(如动态前馈控制)补偿已知扰动。
参考代码 卡尔曼滤波+PID,可以实现滤波降噪 www.youwenfan.com/contentcnn/83865.html
四、扩展应用:卡尔曼滤波+PID+深度学习
- 端到端噪声抑制:用神经网络预测噪声分布,动态调整卡尔曼滤波参数。
- 复杂系统建模:针对高维、强耦合系统,采用深度学习辅助状态估计。
通过卡尔曼滤波与PID的协同,可显著提升控制系统的抗噪性能与动态响应,适用于工业自动化、机器人、自动驾驶等领域。



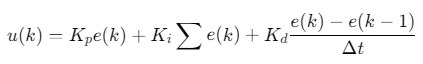

 浙公网安备 33010602011771号
浙公网安备 33010602011771号