EEGNet细读 似乎是最为经典的脑电数据处理模型

论文链接

CNN 卷积神经网络

总的来说，就是有一些输入，然后得到输出，输出一般分为两类：数值和分类。
比如经典的手写数字识别，给一张图片，输出10个概率值或者是0-9的一个确定数字。

CNN总体结构

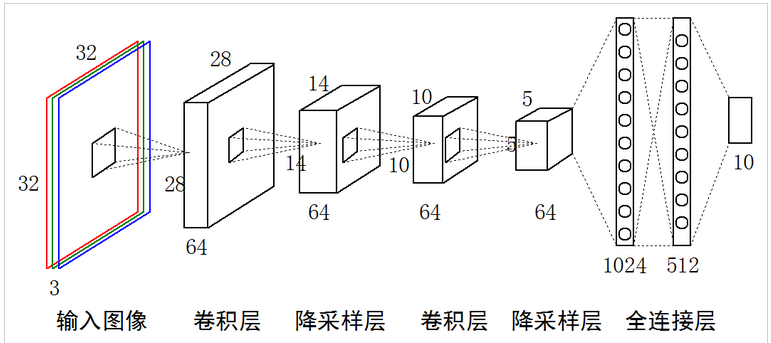
该图从这里上复制过来，其中的降采样层一般被称为池化层，后续我称为池化层

前半部分

从卷积层一直到最一个池化层为止属于前半部分

卷积层

就是拿多个矩阵（似乎一般是3x3的）去和原图像矩阵进行卷积，也就是重叠然后相乘再求和得到一个新值，新值会再组成一个矩阵。
这些矩阵被称为卷积核，它里面的数值会代表着一定的特征，原图像与核进行卷积就相当一个特征捕获的过程，所以这个卷积核会根据需要进行设计。


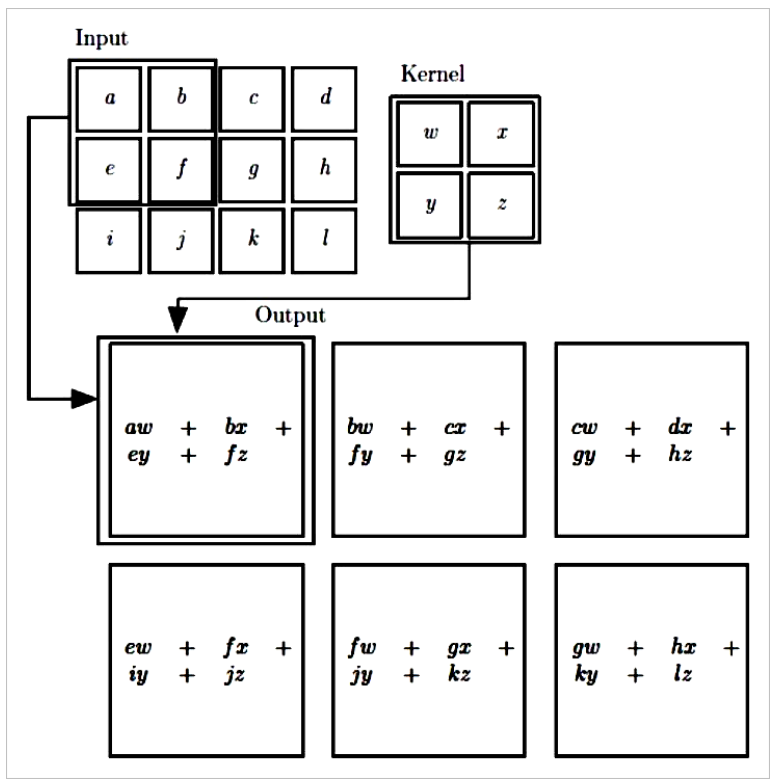
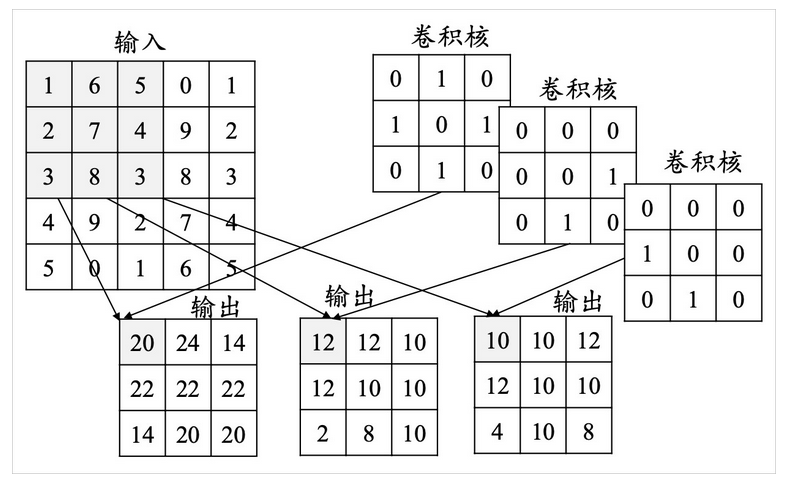
但是上图这个方式会有些小问题，首先很明显这样最后的图像会变小，然后边缘部分不像中间的会与卷积核的所有部分都相乘过，特征捕获不会很完整，一般会先扩充原图像再进行卷积

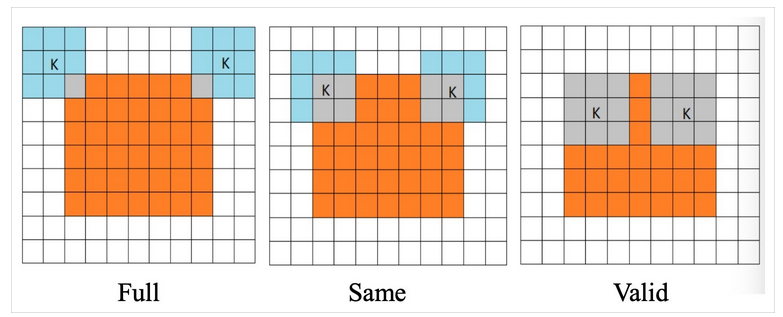
关于怎么在边缘上进行扩充这个我不太清楚，还是请参考这篇文章。

池化层

对于经由卷积层得到的矩阵，通过取几个小方块的某种值作为代表组成新的矩阵，这个过程就是池化，主要是去除大量冗余信息的，当然这样也能顺便去下噪。

后半部分（全连接层）

参考视频
全连接层其实就是个神经网络，似乎诞生得比CNN要早。
简单的说，就是一个由一堆x得到一堆y(或一个y)的过程，如下图：

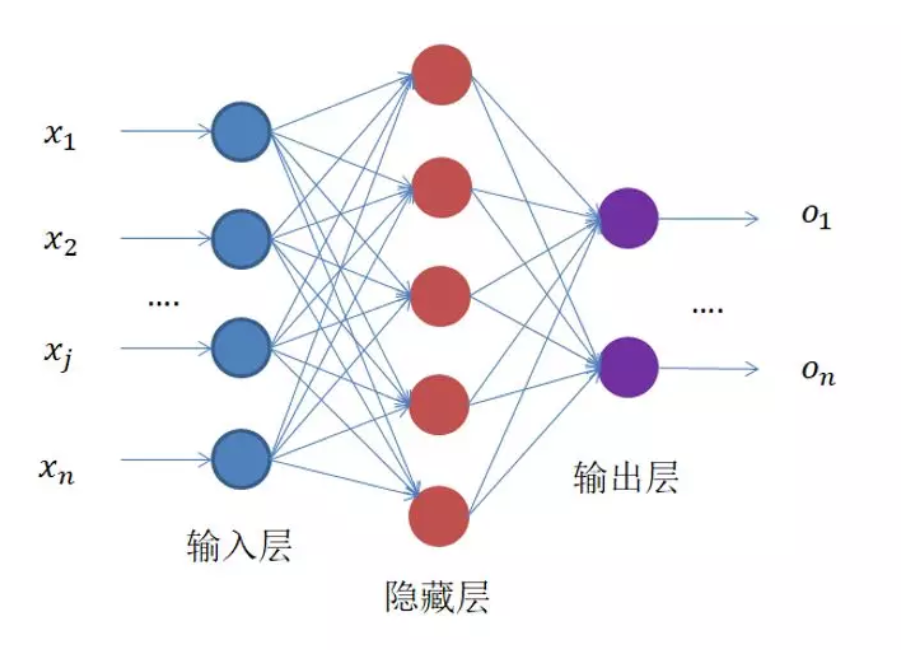
可以看到，输入是一维的，那么在CNN的前半部分得到的最后一个池化层后面的矩阵需要转为一维的，直接粗暴地将不同卷积核卷出来的矩阵按行拼接即可（不知道有没有其他方式）。
隐藏层和输入、输出层的每个小圆圈一般称为神经元，对于输入输出层里面是值，对于隐藏层，里面可以是有激活函数（一般就是relu和其他)，从小球到下一层所有小球的线上面有着权重与偏置，也就是y = ax + b这样的一个线性变化

关于激活函数为什么不能是线性的

如果上图的红色小球里面也是线性变化，那从x到最后的y就只有线性变化了，相当于有没有中间一堆都一样。而且线性的拟合效果不太行。

CNN训练过程

全连接神经网络训练过程（参考链接与参考视频)

如上文所述，从x到y的过程中存在很多的a和b，要训练的就是这些值，那么具体是怎么训练的呢？反向传播

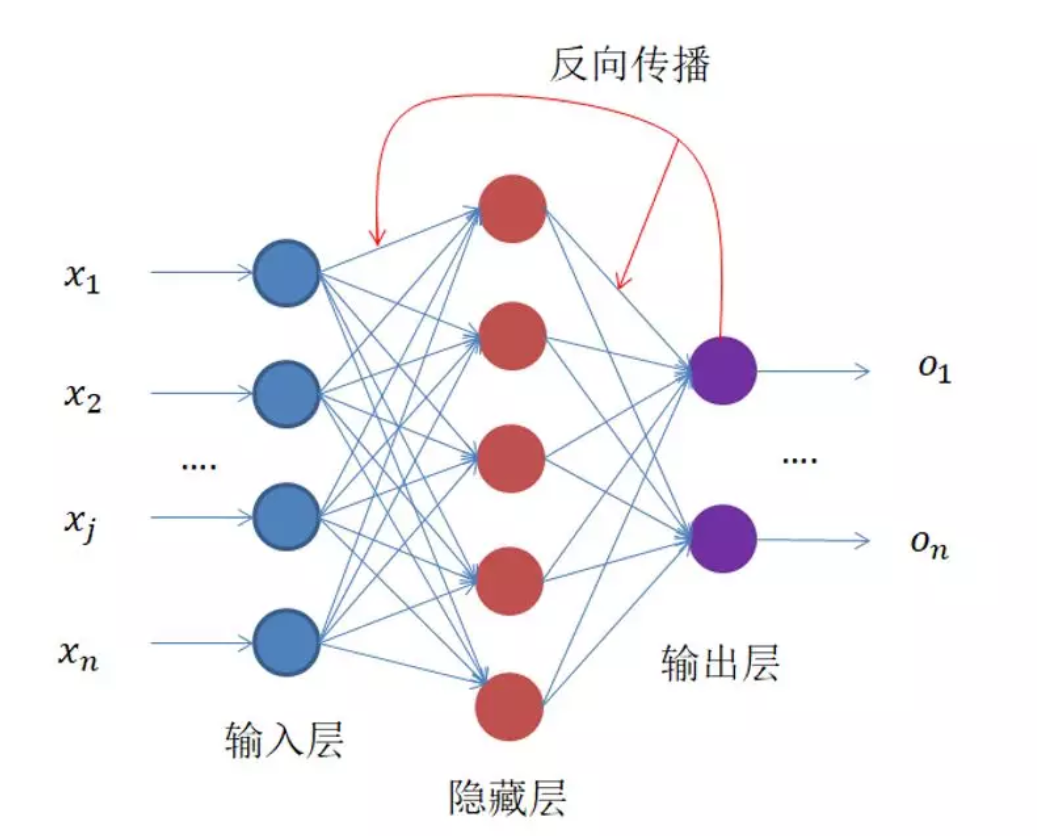
首先有些默认的参数值，模型得到的一堆值和预期值之间有差距，这个差值叫LOSS，LOSS的一些经典定义方式如下：

$ Loss = \sum_{i=1}^{n} (y_i - (wx_i + b))^2 $， $Loss = \sum_{i=1}^{n} \left( x_i^2 w^2 + b^2 + 2x_i wb - 2y_i b - 2x_i y_i w + y_i^2 \right) $ ， $Loss = \sum_{i=1}^{n} \left( A w^2 + B b^2 + C wb - Db - Ew + F \right) $ 通过不断缩小LOSS来优化权重与偏置，那么w和b到底该如何变化的呢？使用**梯度下降法** 设想下面这样的场景：  根据梯度进行调整，每次蠕动一点点最后就能到底部附近，具体来说将loss函数对各参数求偏导，然后各权重进行更新： $w_{i+1} = w - \alpha \frac{\partial f(w)}{\partial w^i}$ b同理，公式中的$\alpha$就是学习率，也就是蠕动的步长，不宜过大。

EEG Net 结构