CSAPP cachelab
cache lab
Part A
写在前面
这部分要求你实现一个模拟缓存运行的C语言程序,支持读,写,修改内存三个操作,其与对于缓存模拟的行为给定的\(csim-ref\)可执行文件一致,最后输出操作完成后的缓存命中,未命中,替换的次数。缓存的组数,行数,每一行的字节数在执行时以参数给出,替换策略使用\(LRU\)(least-recently used),即每次替换块内离上一次引用时间最久的块
但是本部分不要求你输出访问时具体的值,你只需要统计这次操作是否命中,未命中,替换
在运行的时候,我们采用了一下的选项来传递参数
linux> ./csim-ref [-hv] -s <s> -E <E> -b <b>-t <tracefile>
其中-h -v两个选项可选可不选,且后面没有参数,分别表示打印使用方法,和运行时是否可见化地输出每次缓存访问的结果
-s -E -b 后接一个参数,分别表示组数,每组行数,每行字节数
-t 后接字符串参数,表示读入文件的路径
读入部分
怎么感觉是Part A 里面最难的部分(
首先为了从选项中读出参数,我们在linux系统下需要使用\(getopt\)函数,该函数原型如下
int getopt(int argc, char * const argv[], const char *optstring)
其中\(argc\),\(argv\)为\(main\)函数的参数,分别代表参数个数和参数列表
\(optstring\)为选项字符串,举例来说,getopt(argc, argv, "hvs:E:b:t:")就表示有-h -v -s -E -b -t 这几个选项,其中-s -E -b -t 若选择的话,后面必须带有参数
该函数返回值为选项的ASCII码,同时,包含该函数的 <unistd.h> 和 <getopt.h> 中有名为 \(optarg\)的指针变量,在每次使用\(getopt\)时,若该选项有参数,就会被更新为该参数的字符串指针
由此不难写出读入函数
int op;
FILE *fp;
while ((op = getopt(argc, argv, "hvs:E:b:t:")) != EOF) {
if (op == 'h') {
Help();
return 0;
}
if (op == 'v') {
v = 1;
continue;
}
if (op == 's') {
s = atoi(optarg);//atoi 在 stdlib.h中,传入一个字符串开头的指针,将其转换为整数
S = (1 << s);
continue;
}
if (op == 'E') {
E = atoi(optarg);
continue;
}
if (op == 'b') {
b = atoi(optarg);
B = (1 << b);
continue;
}
if (op == 't') {
fp = fopen(optarg, "r");//文件指针指向参数标明的文件
continue;
}
Help();
return 0;//其它异常参数符
}
每次操作分为以下四类:
I address size表示取address地址的size位指令L address size表示加载address地址开始的size位数据S address size表示向address地址开始的size位写数据L address size表示修改address地址的size位数据
但是这部分只要我们用缓存处理数据信息,同时又不需要真正地对缓存进行读写,只是模拟是否命中和替换这个过程即可
所以 I操作完全没用, L 和S操作完全等价 (无语
char opt[5];
size_t ad;
int siz;
while (fscanf(fp, "%s %lx,%d", opt, &ad, &siz) != EOF) {
++curtime;
if (v) {
printf("%c %lx,%d\n", opt[0], ad, siz);
}
if (opt[0] == 'I') continue;
if (opt[0] == 'L') Load(ad);
if (opt[0] == 'S') Store(ad);
if (opt[0] == 'M') Modify(ad);
}
缓存的相关结构
由于本部分缓存大小未知,需要动态分配内存,这里实现上使用了指针加 malloc动态分配空间
struct row {
int valid, flag, dfn;
//有效位 标志位 上次更新的时间戳
};//一行
typedef struct row* set;//一组
typedef set* cache;//整个缓存
cache c;
void Cache_init() {
c = (cache)malloc(sizeof(set) * S);//分配S个组的空间
for (int i = 0; i < S; i++) {
c[i] = (set)malloc(sizeof(struct row) * E);//每一组分配E行的空间
for (int j = 0; j < E; j++) {
c[i][j].valid = 0;
c[i][j].flag = c[i][j].dfn = -1;
}
}
}
缓存的读写
我们先对地址使用位运算得到该地址应该被分配到的组数,标识位和偏移量(偏移量好像没用)
为了维护某一组内是否有该地址对应的标志位,我们可以采用平衡树,但是E一般都比较小,没有这个必要(不是我懒得写了),直接E行依遍历比较就行
如果存在标识符相同且有效的,那么发生缓存命中,修改这一行的时间戳,直接返回即可
否则缓存未命中,我们优先找该组空的行,若存在,直接放入并更新时间戳,将其有效位设置为1,此时未命中,也未发生替换
如空的行不存在,我们就将该组中时间戳最小的行替换为需要访问的数据,同样更新时间戳即可,此时未命中并发生替换
void Load(int ad) {
//m = t + s + b
// int _b = ad & ((1 << b) - 1);
int _s = (ad >> b) & ((1 << s) - 1);
int _t = ad >> (s + b);
struct row* r = c[_s];
for (int i = 0; i < E; i++) {
if ((r + i)->valid && (r + i)->flag == _t) {//缓存命中
if (v) puts("hit");
++hit;
(r + i)->dfn = curtime;
return;
}
}
struct row* evicp = r;
for (int i = 1; i < E; i++) {
if ((r + i)->dfn == -1 || (r + i)->dfn < evicp->dfn) {//优先使用空行
evicp = r + i;
}
}
miss++;
printf("miss");
if (evicp->dfn != -1) {
evic++;
if (v) printf(" eviction");
}//发生了替换
putchar('\n');
evicp->dfn = curtime; evicp->valid = 1; evicp -> flag = _t;
return;
}
写入和加载的行为完全一致,修改逻辑类似,注意读的时候就在缓存中只算命中缓存一次,就不展开了
void Store(int ad) {
Load(ad);
}
void Modify(int ad) {
//m = t + s + b
// int _b = ad & ((1 << b) - 1);
int _s = (ad >> b) & ((1 << s) - 1);
int _t = ad >> (s + b);
struct row *r = c[_s];
for (int i = 0; i < E; i++) {
if ((r + i)->valid && (r + i)->flag == _t) {
if (v) puts("hit");
hit += 2;
(r + i)->dfn = curtime;
return;
}
}
struct row* evicp = r;
for (int i = 1; i < E; i++) {
if ((r + i)->dfn == -1 || (r + i)->dfn < evicp->dfn) {
evicp = r + i;
}
}
miss++; hit++;
if (v) puts("miss");
if (evicp->dfn != -1) {
evic++;
if (v) printf(" eviction");
}
puts(" hit");
evicp->dfn = curtime; evicp->valid = 1; evicp -> flag = _t;
return;
}
代码
主体已经完成了,再加上使用说明即可
#include "cachelab.h"
#include <unistd.h>
#include <stdio.h>
#include <stdlib.h>
#include <getopt.h>
int E, s, S, b, B, v, t;
const int m = 64;
int curtime;
int hit, miss, evic;
struct row {
int valid, flag, dfn;
//有效位 标志位 上次更新的时间戳
};//一行
typedef struct row* set;//一组
typedef set* cache;//整个缓存
cache c;
void Cache_init() {
c = (cache)malloc(sizeof(set) * S);//分配S个组的空间
for (int i = 0; i < S; i++) {
c[i] = (set)malloc(sizeof(struct row) * E);//每一组分配E行的空间
for (int j = 0; j < E; j++) {
c[i][j].valid = 0;
c[i][j].flag = c[i][j].dfn = -1;
}
}
}
/*
Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>
Options:
-h Print this help message.
-v Optional verbose flag.
-s <num> Number of set index bits.
-E <num> Number of lines per set.
-b <num> Number of block offset bits.
-t <file> Trace file.
Examples:
linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace
linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace
*/
void Help() {
printf(
"Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n"
"Options:\n"
" -h Print this help message.\n"
" -v Optional verbose flag.\n"
" -s <num> Number of set index bits.\n"
" -E <num> Number of lines per set.\n"
" -b <num> Number of block offset bits.\n"
" -t <file> Trace file.\n"
"Examples:\n"
" linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n"
" linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n"
);
}
void Load(int ad) {
//m = t + s + b
// int _b = ad & ((1 << b) - 1);
int _s = (ad >> b) & ((1 << s) - 1);
int _t = ad >> (s + b);
struct row* r = c[_s];
for (int i = 0; i < E; i++) {
if ((r + i)->valid && (r + i)->flag == _t) {//缓存命中
if (v) puts("hit");
++hit;
(r + i)->dfn = curtime;
return;
}
}
struct row* evicp = r;
for (int i = 1; i < E; i++) {
if ((r + i)->dfn == -1 || (r + i)->dfn < evicp->dfn) {//优先使用空行
evicp = r + i;
}
}
miss++;
printf("miss");
if (evicp->dfn != -1) {
evic++;
if (v) printf(" eviction");
}//发生了替换
putchar('\n');
evicp->dfn = curtime; evicp->valid = 1; evicp -> flag = _t;
return;
}
void Store(int ad) {
Load(ad);
}
void Modify(int ad) {
//m = t + s + b
// int _b = ad & ((1 << b) - 1);
int _s = (ad >> b) & ((1 << s) - 1);
int _t = ad >> (s + b);
struct row *r = c[_s];
for (int i = 0; i < E; i++) {
if ((r + i)->valid && (r + i)->flag == _t) {
if (v) puts("hit");
hit += 2;
(r + i)->dfn = curtime;
return;
}
}
struct row* evicp = r;
for (int i = 1; i < E; i++) {
if ((r + i)->dfn == -1 || (r + i)->dfn < evicp->dfn) {
evicp = r + i;
}
}
miss++; hit++;
if (v) puts("miss");
if (evicp->dfn != -1) {
evic++;
if (v) printf(" eviction");
}
puts(" hit");
evicp->dfn = curtime; evicp->valid = 1; evicp -> flag = _t;
return;
}
int main(int argc, char *argv[]){
int op;
FILE *fp;
while ((op = getopt(argc, argv, "hvs:E:b:t:")) != EOF) {
if (op == 'h') {
Help();
return 0;
}
if (op == 'v') {
v = 1;
continue;
}
if (op == 's') {
s = atoi(optarg);//atoi 在 stdlib.h中,传入一个字符串开头的指针,将其转换为整数
S = (1 << s);
continue;
}
if (op == 'E') {
E = atoi(optarg);
continue;
}
if (op == 'b') {
b = atoi(optarg);
B = (1 << b);
continue;
}
if (op == 't') {
fp = fopen(optarg, "r");//文件指针指向参数标明的文件
continue;
}
Help();
return 0;//其它异常参数符
}
Cache_init();//缓冲初始化,动态分配空间
char opt[5];
size_t ad;
int siz;
while (fscanf(fp, "%s %lx,%d", opt, &ad, &siz) != EOF) {
++curtime;
if (v) {
printf("%c %lx,%d\n", opt[0], ad, siz);
}
if (opt[0] == 'I') continue;
if (opt[0] == 'L') Load(ad);
if (opt[0] == 'S') Store(ad);
if (opt[0] == 'M') Modify(ad);
}
printSummary(hit, miss, evic);
return 0;
}
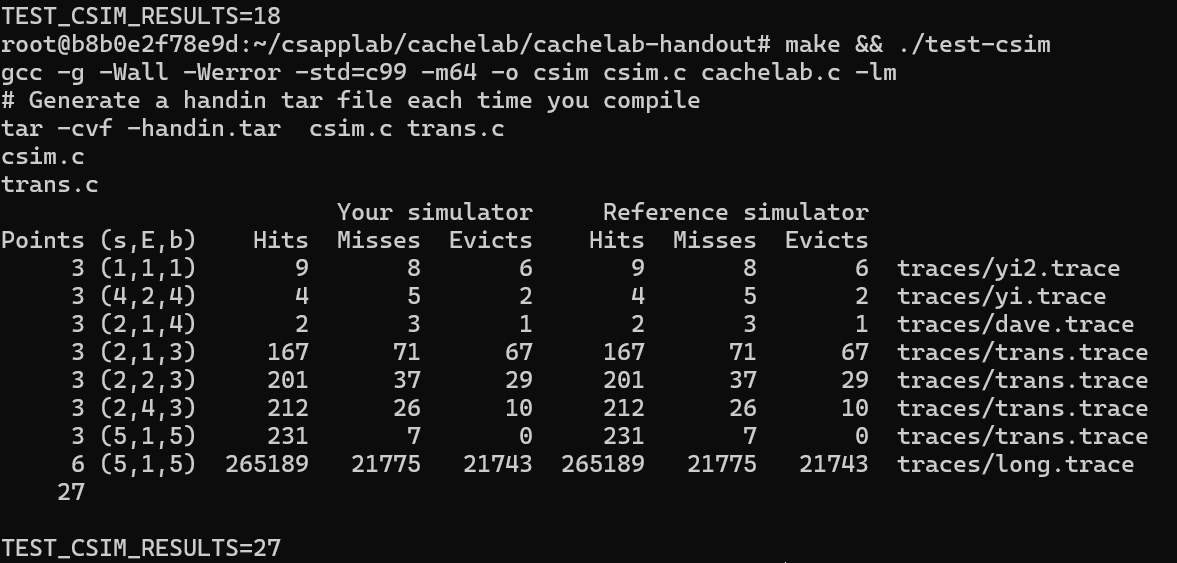
使用 make && ./test-csim得到以下结果
Part B
写在前面
有\(32 \times 32\), \(64 \times 64\), \(61 \times 67\) 三个矩阵\(A\),你需要使用C实现矩阵转置得到矩阵\(B\),要求使得参数为\((s=5, E=1, b=5)\)的缓存产生的不命中次数小于一个给定值,不能自己定义数组,最多使用12个局部变量
手算发现,该缓存有一个32块,每块一行,每行能存储8个int,方便起见,以下称一块为一行,同时使用0-index
通过访问目录下的\(trace.f1\)(题目给出的不加优化的转置代码的缓存行为跟踪)发现,\(A\)的起始地址为\(0x0010d080\),\(B\)的起始地址为\(0x0014d080\),刚好相差\(2^{18}\),这说明在下标相同时,\(A[i][j]\)和\(B[i][j]\)会被分配到相同的一行内,只是标志位不同;同时二者的起始地址都是32的倍数,说明\(A[i][8k+0]\)到\(A[i][8k+7]\)都在一行里面,\(B\)也同理
题目给出的最原始的转置函数如下
void trans(int M, int N, int A[N][M], int B[M][N])
{
int i, j, tmp;
for (i = 0; i < N; i++) {
for (j = 0; j < M; j++) {
tmp = A[i][j];
B[j][i] = tmp;
}
}
}
注意先通过 sudo apt install valgrind 安装 valgrind
$ 32 \times 32 $
本部分要求缓存未命中次数小于300次
先在目录下使用make && ./test-trans -M 32 -N 32对原始函数缓存访问效率进行测试,结果如下

发现该函数对于缓存访问相当不友好,我们先搞明白1183次不命中是怎么来的
每隔8个int就会产生一个行的偏移,先画出每个int会被放入缓存的哪一行(不会画图,图是偷的,勿喷)
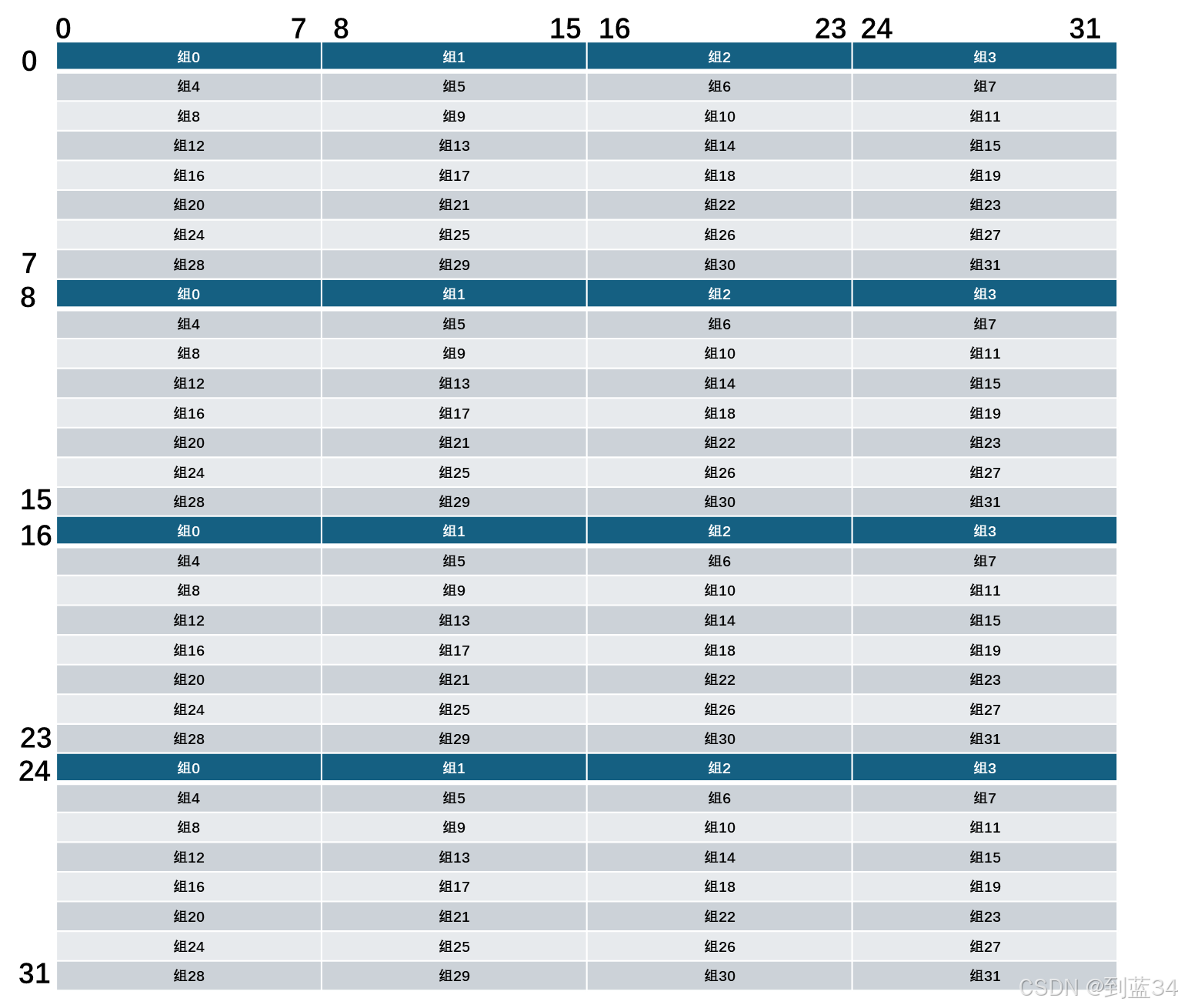
1.对于\(A\)是步长为1的访问,只有在第一次访问一个没有被访问过的组的时候才会不命中,所以会有128次不命中
2.对于\(B\)是步长为32的访问,每一次都不会命中,所以有1024次不命中
3.对于 \(i=j\) 即对角线上的情况,此时\(B[i][i]\)和\(A[i][i]\)所在的组一样,写入\(B[i][i]\)的值的时候,刚好会将\(A\)所在行替换掉,在下一次读取\(A\)的值的时候,会将\(B\)替换掉,这样的情况会发生31次,因为最后一次访问\((31,31)\)后不会再读取\(A\)了
所以一共为128+1024+31=1183次
接下来考虑如何优化,可以使用分块,取块长为8,即每次将一个\(8\times8\)的\(A\)矩阵写入其在\(B\)上对应的位置
这样优化后,\(A\)在块内以步长为1访问,而\(B\)在块内按列顺序访问,每一块会在每一列第一次访问的时候不命中
优化后代码如下
if (M == 32 && N == 32) {
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (ii = i; ii < i + 8; ii++) {
for (jj = j; jj < j + 8; jj++) {
B[jj][ii] = A[ii][jj];
}
}
}
}
}

仍然需要进一步的优化,考虑对角线上的块,在转置的时候会发生对\(B\)进行写入时,替换掉了这一行的\(A\),所以可以使用临时变量保存\(A\)的值,然后放入\(B\)中,这样减少了访问\(A\)这一行后面的元素所需要的一次不命中
if (M == 32 && N == 32) {
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (ii = i; ii < i + 8; ii++) {
a = A[ii][j];
b = A[ii][j + 1];
c = A[ii][j + 2];
d = A[ii][j + 3];
e = A[ii][j + 4];
f = A[ii][j + 5];
g = A[ii][j + 6];
h = A[ii][j + 7];
B[j ][ii] = a;
B[j + 1][ii] = b;
B[j + 2][ii] = c;
B[j + 3][ii] = d;
B[j + 4][ii] = e;
B[j + 5][ii] = f;
B[j + 6][ii] = g;
B[j + 7][ii] = h;
}
}
}
}
结果如下,成功通过此题

\(64\times64\)
本部分要求缓存未命中次数小于1300
再次偷图( 这是左上角\(16 \times 16\)的矩阵
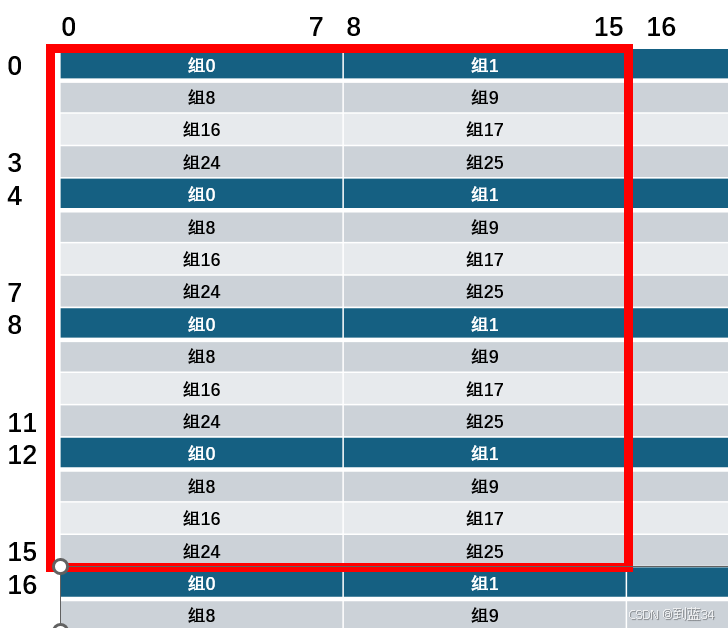
如果我们仍然采用\(8\times8\)分块处理的话,块内会存在严重的抖动,比如\(B\)内部对组0,组8,组16,组24都有两次访问,都会产生一次替换,这导致缓存命中率相当糟糕,实际测试中不命中次数为4611,与未优化的原始代码次数4723几乎没有差别
为了减少\(B\)的抖动,我们尝试使用\(4\times4\)分块
if (M == 64 && N == 64) {
for (i = 0; i < N; i += 4) {
for (j = 0; j < M; j += 4) {
for (ii = i; ii < i + 4; ii++) {
a = A[ii][j];
b = A[ii][j + 1];
c = A[ii][j + 2];
d = A[ii][j + 3];
B[j ][ii] = a;
B[j + 1][ii] = b;
B[j + 2][ii] = c;
B[j + 3][ii] = d;
}
}
}
}
结果如下

有所优化但是还未达到本题要求,采用\(4\times4\)分块的时候,虽然\(B\)的抖动减少了,但是对\(A\)中原本连续8个数的访问变成了两次对4个数的访问,这增加了\(A\)的抖动
到这里就不会了,去看别人博客了(
我们考虑以下的策略
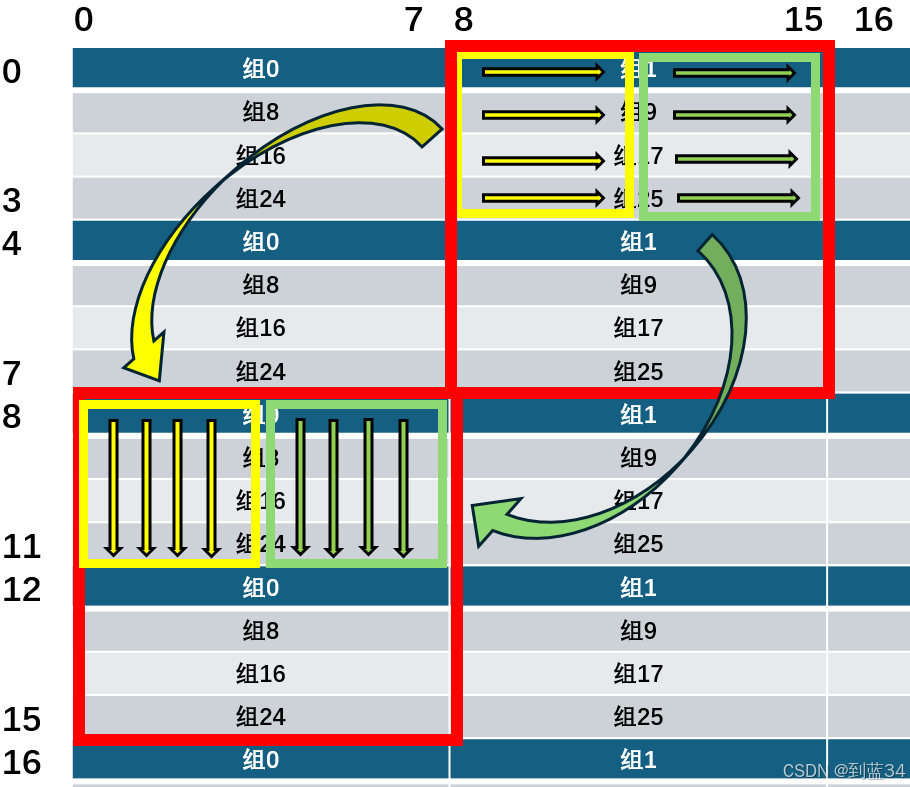
1.先读取\(A\)矩阵\(8\times8\)分块的前4行,将黄色部分和绿色部分分别转置后,直接顺序不变拷贝到\(B\)中,此时未发生缓存替换,只有\(A\)和\(B\)的各4次载入
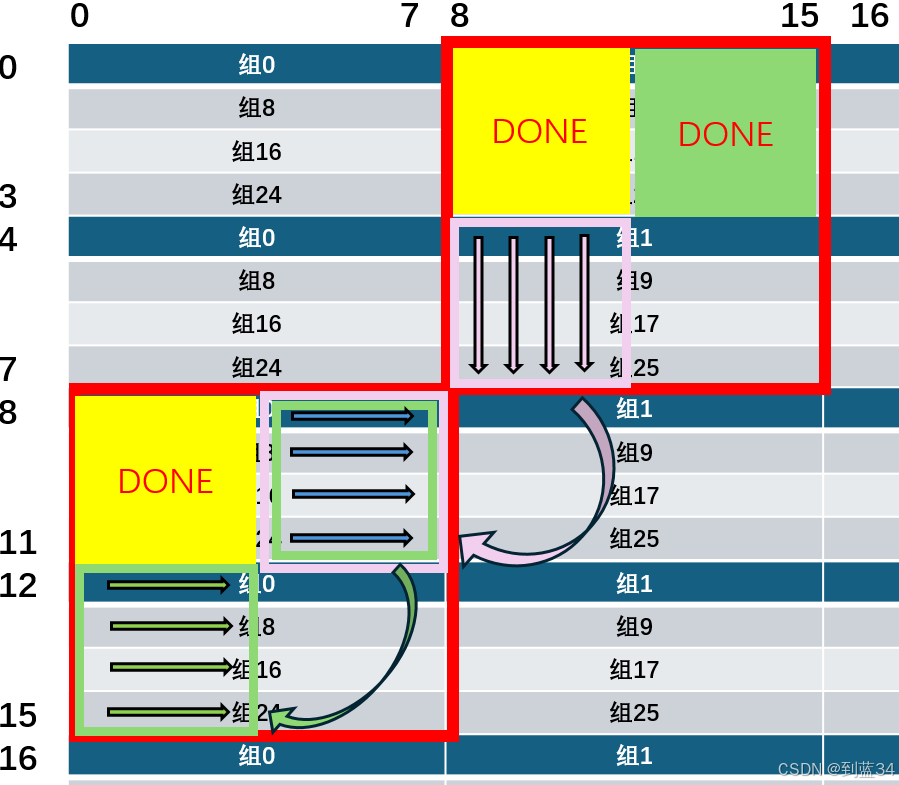
2.使用寄存器暂存未放置正确的绿色部分的一行,然后将粉色部分的一列放置到绿色部分的这一行,接着从寄存器中取值将绿色部分这一行放到正确的位置。绿色部分已经存放在了缓存中,可以直接读取,粉色第一列的时候会发生4次载入,热身缓存,正确放置绿色部分每一行的时候都会产生一次对原本存放\(A\)的组的替换,故一共发生8次缓存不命中
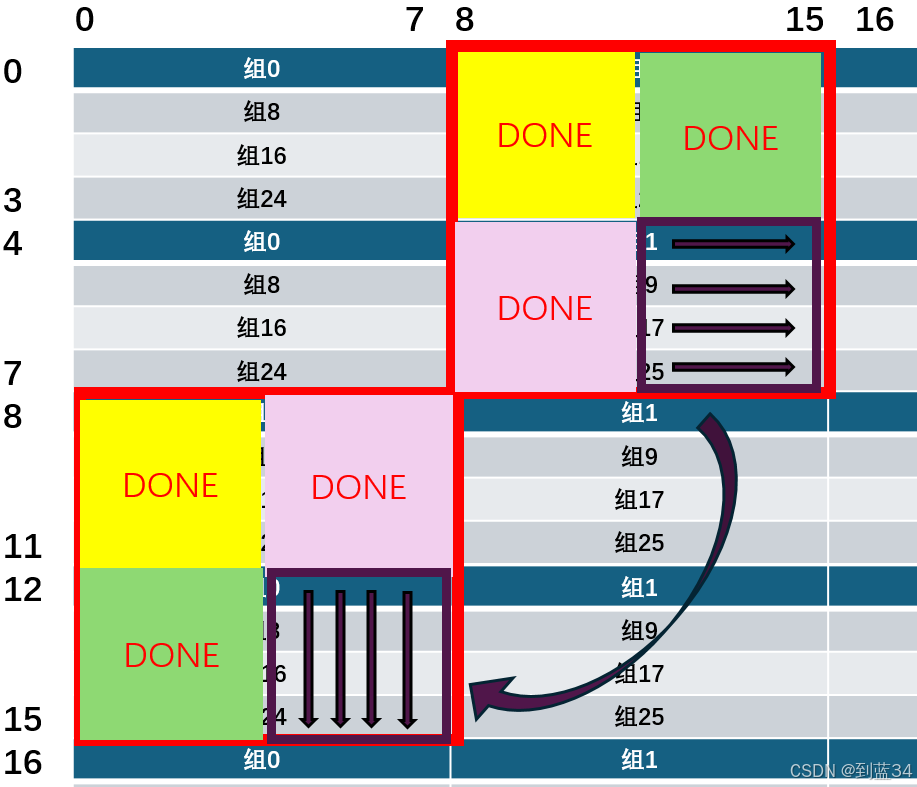
3.最后将紫色部分直接转置到正确位置即可,紫色部分每一行和放置的\(B\)每一列都在缓存中,全部命中
所以对于\(8\times8\)的块,发生了16次不命中,对\(64 \times 64\)的块,理论会有1024次不命中
if (M == 64 && N == 64) {
int i, j, ii;
int a, b, c, d, e, f, g, h;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (ii = i; ii < i + 4; ii++) {
a = A[ii][j];
b = A[ii][j + 1];
c = A[ii][j + 2];
d = A[ii][j + 3];
e = A[ii][j + 4];
f = A[ii][j + 5];
g = A[ii][j + 6];
h = A[ii][j + 7];
B[j][ii] = a;
B[j + 1][ii] = b;
B[j + 2][ii] = c;
B[j + 3][ii] = d;
B[j][ii + 4] = e;
B[j + 1][ii + 4] = f;
B[j + 2][ii + 4] = g;
B[j + 3][ii + 4] = h;
}
for (ii = 0; ii < 4; ii++) {
a = B[j + ii][i + 4];
b = B[j + ii][i + 5];
c = B[j + ii][i + 6];
d = B[j + ii][i + 7];
e = A[i + 4][j + ii];
f = A[i + 5][j + ii];
g = A[i + 6][j + ii];
h = A[i + 7][j + ii];
B[j + ii][i + 4] = e;
B[j + ii][i + 5] = f;
B[j + ii][i + 6] = g;
B[j + ii][i + 7] = h;
B[j + 4 + ii][i] = a;
B[j + 4 + ii][i + 1] = b;
B[j + 4 + ii][i + 2] = c;
B[j + 4 + ii][i + 3] = d;
}
for (ii = i + 4; ii < i + 8; ii++) {
a = A[ii][j + 4];
b = A[ii][j + 5];
c = A[ii][j + 6];
d = A[ii][j + 7];
B[j + 4][ii] = a;
B[j + 5][ii] = b;
B[j + 6][ii] = c;
B[j + 7][ii] = d;
}
}
}
return;
}
运行结果如下,达到了本题的要求

\(67 \times 61\)
本题要求缓存不命中次数小于2000
我们调整参数,发现使用\(16 \times 16\)分块可以通过此题
if (M == 67 && N == 61) {
int i, j, ii,jj;
for (i = 0; i < 61; i += 16) {
for (j = 0; j < 67; j += 16) {
for (ii = i; ii < i + 16 && ii < 61; ii++) {
for (jj = j; jj < j + 16 && jj < 67; jj++) {
B[jj][ii] = A[ii][jj];
}
}
}
}
}
结果如下

代码
点击查看代码
/*
* trans.c - Matrix transpose B = A^T
*
* Each transpose function must have a prototype of the form:
* void trans(int M, int N, int A[N][M], int B[M][N]);
*
* A transpose function is evaluated by counting the number of misses
* on a 1KB direct mapped cache with a block size of 32 bytes.
*/
#include <stdio.h>
#include "cachelab.h"
int is_transpose(int M, int N, int A[N][M], int B[M][N]);
/*
* transpose_submit - This is the solution transpose function that you
* will be graded on for Part B of the assignment. Do not change
* the description string "Transpose submission", as the driver
* searches for that string to identify the transpose function to
* be graded.
*/
char transpose_submit_desc[] = "Transpose submission";
void transpose_submit(int M, int N, int A[N][M], int B[M][N])
{
if (M == 32 && N == 32) {
int i, j, ii;
int a, b, c, d, e, f, g, h;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (ii = i; ii < i + 8; ii++) {
a = A[ii][j];
b = A[ii][j + 1];
c = A[ii][j + 2];
d = A[ii][j + 3];
e = A[ii][j + 4];
f = A[ii][j + 5];
g = A[ii][j + 6];
h = A[ii][j + 7];
B[j ][ii] = a;
B[j + 1][ii] = b;
B[j + 2][ii] = c;
B[j + 3][ii] = d;
B[j + 4][ii] = e;
B[j + 5][ii] = f;
B[j + 6][ii] = g;
B[j + 7][ii] = h;
}
}
}
return;
}
if (M == 64 && N == 64) {
int i, j, ii;
int a, b, c, d, e, f, g, h;
for (i = 0; i < N; i += 8) {
for (j = 0; j < M; j += 8) {
for (ii = i; ii < i + 4; ii++) {
a = A[ii][j];
b = A[ii][j + 1];
c = A[ii][j + 2];
d = A[ii][j + 3];
e = A[ii][j + 4];
f = A[ii][j + 5];
g = A[ii][j + 6];
h = A[ii][j + 7];
B[j][ii] = a;
B[j + 1][ii] = b;
B[j + 2][ii] = c;
B[j + 3][ii] = d;
B[j][ii + 4] = e;
B[j + 1][ii + 4] = f;
B[j + 2][ii + 4] = g;
B[j + 3][ii + 4] = h;
}
for (ii = 0; ii < 4; ii++) {
a = B[j + ii][i + 4];
b = B[j + ii][i + 5];
c = B[j + ii][i + 6];
d = B[j + ii][i + 7];
e = A[i + 4][j + ii];
f = A[i + 5][j + ii];
g = A[i + 6][j + ii];
h = A[i + 7][j + ii];
B[j + ii][i + 4] = e;
B[j + ii][i + 5] = f;
B[j + ii][i + 6] = g;
B[j + ii][i + 7] = h;
B[j + 4 + ii][i] = a;
B[j + 4 + ii][i + 1] = b;
B[j + 4 + ii][i + 2] = c;
B[j + 4 + ii][i + 3] = d;
}
for (ii = i + 4; ii < i + 8; ii++) {
a = A[ii][j + 4];
b = A[ii][j + 5];
c = A[ii][j + 6];
d = A[ii][j + 7];
B[j + 4][ii] = a;
B[j + 5][ii] = b;
B[j + 6][ii] = c;
B[j + 7][ii] = d;
}
}
}
return;
}
if (M == 61 && N == 67) {
int i, j, ii,jj, tmp;
for (i = 0; i < N; i += 16) {
for (j = 0; j < M; j += 16) {
for (ii = i; ii < i + 16 && ii < N; ii++) {
for (jj = j; jj < j + 16 && jj < M; jj++) {
tmp = A[ii][jj];
B[jj][ii] = tmp;
}
}
}
}
}
}
/*
* You can define additional transpose functions below. We've defined
* a simple one below to help you get started.
*/
/*
* trans - A simple baseline transpose function, not optimized for the cache.
*/
char trans_desc[] = "Simple row-wise scan transpose";
void trans(int M, int N, int A[N][M], int B[M][N])
{
int i, j, tmp;
for (i = 0; i < N; i++) {
for (j = 0; j < M; j++) {
tmp = A[i][j];
B[j][i] = tmp;
}
}
}
/*
* registerFunctions - This function registers your transpose
* functions with the driver. At runtime, the driver will
* evaluate each of the registered functions and summarize their
* performance. This is a handy way to experiment with different
* transpose strategies.
*/
void registerFunctions()
{
/* Register your solution function */
registerTransFunction(transpose_submit, transpose_submit_desc);
/* Register any additional transpose functions */
registerTransFunction(trans, trans_desc);
}
/*
* is_transpose - This helper function checks if B is the transpose of
* A. You can check the correctness of your transpose by calling
* it before returning from the transpose function.
*/
int is_transpose(int M, int N, int A[N][M], int B[M][N])
{
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < M; ++j) {
if (A[i][j] != B[j][i]) {
return 0;
}
}
}
return 1;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号