有正能量的网络流

网络流

https://chuna2.787528.xyz/chara-/p/18722684

题目

https://vjudge.net/contest/780784

D

令 \(m\times n\) 的矩阵 \(A\) 满足 \(a_{i,j}=[l_i\le j\le r_i]\)，原问题是

\(A\bm x\ge \bm{d}\)，\(n\) 个 \(x_i\ge 0\)，求 \(\min(\bm{c}^{\mathrm{T}}\bm x)\)，把它对偶一下，就变成了

\(A^{\mathrm{T}}\bm y\le \bm{c}\)，\(m\) 个 \(y_i\ge 0\)，求 \(\max(\bm{d}^{\mathrm{T}} \bm y)\)。

发现 \(A^{\mathrm{T}}\) 一列有一段 \(1\)，为了契合费用流考虑把它差分。但是只有等式才能差分，于是我们新增 \(n\) 个变量 \(l_i\)，使得 \(A^{\mathrm{T}}\bm y+\bm{l}=\bm{c}\)，且 \(l_i\ge 0\)。然后将第 \(i\) 行减去第 \(i-1\) 行，写出来大概是

\[\sum_{j=1}^{m}a_{i,j}y_j+l_i-\sum_{j=1}^{m}a_{i-1,j}y_j-l_{i-1}=c_i-c_{i-1}\\ \sum_{j=1}^{m}(-1\ \text{or}\ 0\ \text{or}\ 1)y_j+l_i-l_{i-1}=c_i-c_{i-1} \]

这样每个变量的系数都是恰好一个 \(1\) 和 \(-1\)，所以就可以直接用费用流解决了。

j

\(T\) 里减，\(T\) 外加，每条边是一个变量，钦定树边 \(-x_i\)，非树边 \(+x_i\)。目标 \(\min(\bm{d}^{\mathrm{T}}\bm x)\)，条件为 \(w_i-x_i\le w_j+x_j\Rightarrow x_i+x_j\ge \max(w_i-w_j,0)\)，如果第 \(i\) 条边是树边，第 \(j\) 条边是非树边。

相当于有一个 \(O(nm)\times m\) 的系数矩阵 \(A\)，条件为 \(A\bm x\ge \bm{w}\)，\(x_i\ge 0\)，目标 \(\min(\bm{d}^{\mathrm{T}}\bm x)\)。直接对偶得到 \(A^{\mathrm{T}} \bm y\le \bm{d}\)，目标 \(\max(\bm{w}^{\mathrm{T}}\bm y)\)。注意到 \(A^{\mathrm{T}}\) 一列仅有两个 \(1\)，一个是第 \(i\) 行，一个是第 \(j\) 行，不妨假设第 \(i\) 条边是树边，第 \(j\) 条边是非树边。为了转换成费用流形式，不妨将所有树边的系数全部取反，那么第 \(i\) 行就变成了 \(-1\)，对应的限制变成 \(\ge -d_{i}\)。直接套费用流即可。

M

先来点前置知识。

在多元函数 \(f(x_1,x_2,\cdots,x_n)\) 中，如果

\[\displaystyle \lim_{\Delta x_i\to 0}\frac{f(x_1,\cdots,x_i+\Delta x_i,\cdots,x_n)-f(x_1,x_2,\cdots,x_n)}{\Delta x_i} \]

存在，则称其为函数在点 \(x_1,x_2,\cdots,x_n\) 上对 \(x_i\) 的偏导数，记作 \(\frac{\partial}{\partial x_i}f(x_1, x_2, \cdots, x_n)\)。

计算法则：求偏导时，将其他自变量看作常数。如 \(f(x,y)=x^2y+7xy^2\) 对 \(x\) 的偏导数 \(\frac{\partial}{\partial x}f(x,y)=2xy+7y^2\)。

定义一个多元函数的梯度是一个向量，\(\nabla f(x_1,x_2,\cdots,x_n)=(\frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2},\cdots,\frac{\partial}{\partial x_n})\)。梯度的方向是函数在该点处变化最快的方向，也就是函数值增长最快的方向，而梯度的模（长度）则表示函数在该方向上的变化率（增长率）的大小。

具体什么用不用管，只需要知道想要求一个多元函数的极值点，只需令 \(\nabla=0\)，列出方程组并求解，得到的点就有可能是极值点。

拉格朗日乘数法。有一个 \(n\) 元函数 \(f(\boldsymbol x)\) 和 \(m\) 条限制，第 \(i\) 条形如 \(g_i(\boldsymbol x)=0\)，求出在满足所有限制下 \(f\) 的极值点。拉格朗日乘数法指出，可以添加拉格朗日乘子 \(\boldsymbol\lambda=(\lambda_1,\lambda_2,\cdots,\lambda_m)\) 并构造拉格朗日函数

\[L(\boldsymbol x,\boldsymbol \lambda)=f(\boldsymbol x)-\sum_{i=1}^{m}\lambda_i g_i(\boldsymbol x) \]

声称这个函数的极值点和 \(f\) 一样，为了求解其极值点，只需解方程

\[\left\{\begin{matrix} \nabla_{\boldsymbol x}L(\boldsymbol x,\boldsymbol \lambda)=0 \\ \nabla_{\boldsymbol\lambda} L(\boldsymbol x,\boldsymbol \lambda)=0 \end{matrix}\right. \]

拉格朗日乘数法将条件极值转为单独的一个函数极值。更深层次来说，拉格朗日函数是条件极值的对偶问题。

---

在本题当中，目标为求出 \(f(\boldsymbol x)=\displaystyle \sum_{i=1}^{m}x_i^2c_i\) 的最小值，限制是

\[g_i(\boldsymbol x)=\sum_{e_j=(* ,i)}x_j-\sum_{e_j=(i,*)}x_j+ \left\{\begin{matrix} 1 & i=1\\ 0 & 1<i<n\\ -1 & i=n \end{matrix}\right. \]

然后按照上文构造拉格朗日函数，解方程

\[\def\l{\lambda} \left\{\begin{matrix} \frac{\partial}{\partial x_i}L(\boldsymbol x)= 2c_ix_i+\l_u-\l_v=0\\ \frac{\partial}{\partial \l_i}L(\boldsymbol x) =g_i(\boldsymbol x)=0\\ \end{matrix}\right. \]

高斯消元，\(n+m\) 个变量，\(n+m\) 个方程。

G

不妨假设 \(b_i\le b_j\)，那么限制变为 \(a_i,a_j\ge b_i,\max(a_i,a_j)\ge b_j\)。首先对于第一个可以先将不满足的 \(a\) 加到 \(b_i\)，所以只需处理第二个。我们将 \(a<b\) 的看作 A 类，\(a\ge b\) 的看作 B 类，那么 \(i\) 一定是 B 类，如果 \(j\) 也是 B 类这个限制就没用了，所以 \(j\) 是 A 类。

同时我们发现，\(a_j\) 只要变到 \(b_j\) 所有跟 \(j\) 有关的限制都没了，所以可以建出以下图。

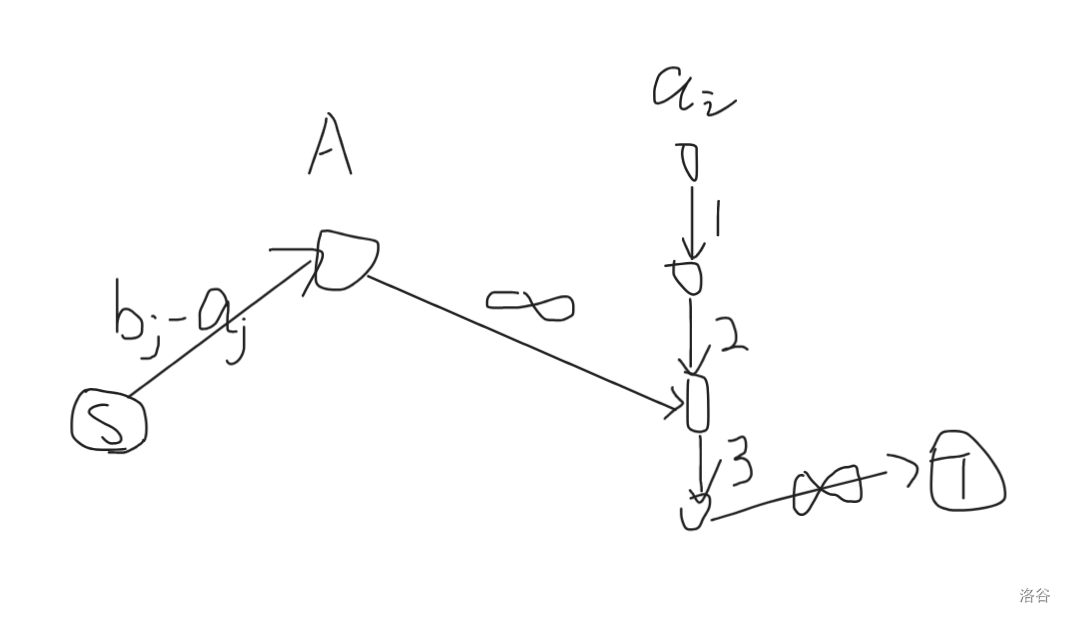
本质上还是一种切糕，要么直接让 \(b_j=a_j\)，要么让 \(a_i+(b_j-a_i)\)。并且容易发现 \(a_i\) 不可能割多条边。所以最终点数 \(O(nV)\)，边数 \(O(nV+m)\)。