浅谈虚树
闲话
看到这篇博客的人教教我定语从句。
The book the cover of which is red is mine.
算法介绍
虚树简介
虚树处理用途较为单一，都是对一棵树上的若干关键点这一形式的题目进行的处理。一般情况下，当关键点很少的时候，虚树的用途就会很大。
假设对于一棵树上，有 \(k\) 个关键点，而我们只在乎关键点之间的路径构成的信息，并且一条路径上的信息比较容易处理，那我们就可以建出虚树。
虚树的关键优化点在于，他用与 \(k\) 相关的事件，把一条路径压缩成虚树上的一条边，达到缩小数据规模的目的。
虚树构建
考虑下面这一颗树。树的蓝色节点是关键点，树的红色节点是在虚树上但不是关键点的节点。
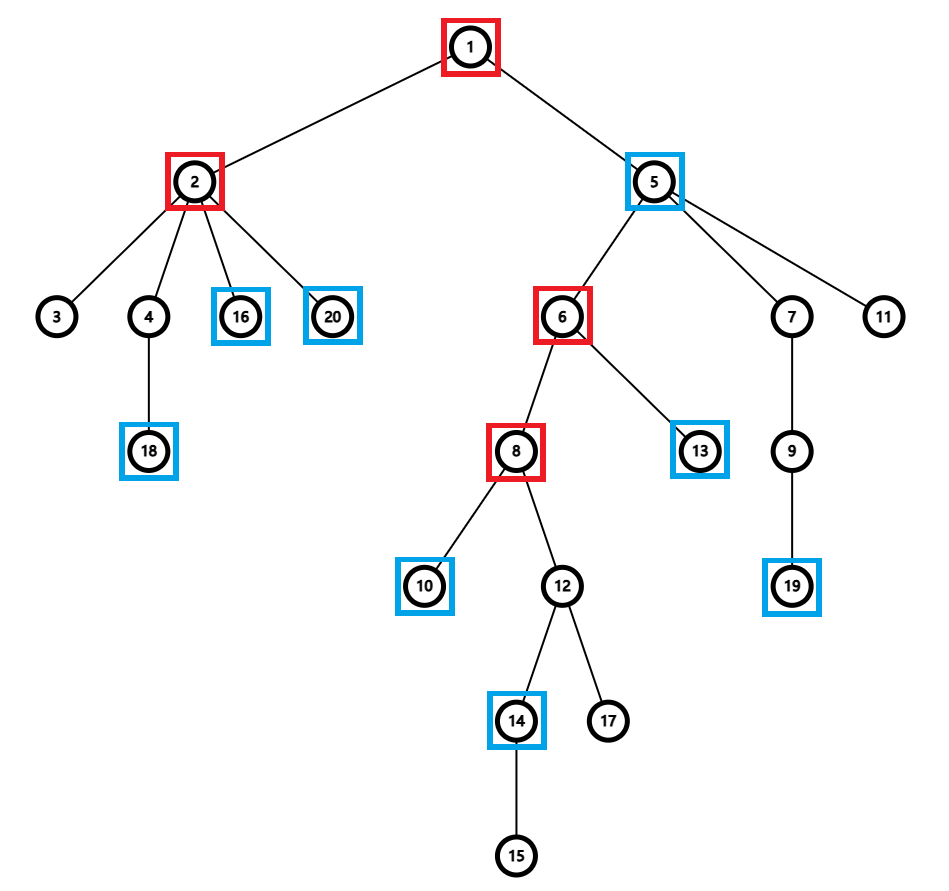
接下来证明一个引理。
引理：将关键节点按照 dfn 序排序，设 \(S\) 集合为所有关键节点与相邻两个关键节点 LCA 构成的点集，那么 \(S\) 集合与虚树点集相等。
证明
假设虚树点集为 $T$，有两个方向。
- \(T\) 包含 \(S\)
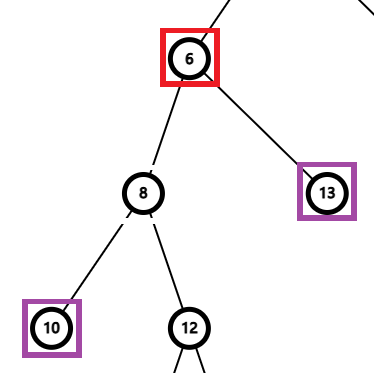
反证，如果存在 \(x \in S\) 但 \(x \notin T\) 的点 \(x\)，显然 \(x\) 子树内存在两个关键点，这两个关键点的 \(LCA\) 等于 \(x\)，也就是这两个点在 \(x\) 的不同儿子的子树里。比如下图中的两个紫点关键点和一个红点 \(x\)。
显然，如果 \(x\) 不在虚树点集中的话，这两个关键点之间的祖先关系会错乱，矛盾。
- \(S\) 包含 \(T\)
反证，假设存在 \(x \notin S\) 但 \(x \in T\) 的点 \(x\)，那么 \(x\) 子树内的所有关键点都属于同一个儿子的子树，这种点加入虚树，一定只有一个儿子，显然可以去除，不符合虚树点数最小的定义，矛盾。
因此，我们容易得到虚树的点集。考虑连边，我们对 \(S\) 点集按照 DFN 排序，然后从左往右扫。
假设当前扫到了点 \(p_i\)，我们要找到 \(p_i\) 的父亲并与这个点连边。显然，这个点应该是 \(q\)，其中 \(\operatorname{LCA}(p_i, q)\) 深度最大。（因为这个点是 \(q\) 最后一次与其他关键点发生分支，那接下来一定是一条链，可以压缩成虚树上的一条边）
容易发现 \(q = p_{i - 1}\)，因此我们把 \(p_{i - 1}\) 向 \(p_i\) 连边即可。
虚树代码
虚树代码
int build(vector<int> &s) {
sort(s.begin(), s.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
vector<int> tmp; tmp.push_back(s[0]);
for (int i = 1; i < (int) s.size(); i ++) {
int c = getLCA(s[i - 1], s[i]);
tmp.push_back(s[i]), tmp.push_back(c);
}
sort(tmp.begin(), tmp.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
int m = unique(tmp.begin(), tmp.end()) - tmp.begin();
for (int i = 1; i < m; i ++) {
int c = getLCA(tmp[i - 1], tmp[i]);
re[c].push_back({tmp[i], d[tmp[i]] - d[c]});
re[tmp[i]].push_back({c, d[tmp[i]] - d[c]});
}
s = tmp;
return tmp[0];
}
例题讲解
P4103 大工程
题目描述
国家有一个大工程，要给一个非常大的交通网络里建一些新的通道。
我们这个国家位置非常特殊，可以看成是一个单位边权的树，城市位于顶点上。
在 \(2\) 个国家 \(a,b\) 之间建一条新通道需要的代价为树上 \(a,b\) 的最短路径的长度。
现在国家有很多个计划，每个计划都是这样，我们选中了 \(k\) 个点，然后在它们两两之间 新建 \(\dbinom{k}{2}\) 条新通道（任意两点间都新建 \(1\) 条）。
现在对于每个计划，我们想知道：
- 这些新通道的代价和。
- 这些新通道中代价最小的是多少。
- 这些新通道中代价最大的是多少。
先建出虚树。我们设虚树上的一条边，权值为在原树上的路径长度，设 \(s_u\) 表示 \(u\) 在虚树上的子树大小。分别考虑：
-
代价和：对于虚树上一个非根节电 \(u\)，考虑 \(u \to fa_u\) 这条边。它贡献了 \(s_u \times (k - s_u)\) 次，贡献为 \(w \times s_u \times (k - s_u)\)。
-
代价最小：类似于 DP 求直径，设 \(mn_u\) 表示从 \(u\) 到 \(u\) 子树内一关键点，这是很好算的，那对于每条路径，我们在 \(\text{LCA}\) 处通过 \(mn\) 数组计算贡献。
-
代价最大：类似于 DP 求直径，设 \(mx_u\) 表示从 \(u\) 到 \(u\) 子树内一关键点，这是很好算的，那对于每条路径，我们在 \(\text{LCA}\) 处通过 \(mx\) 数组计算贡献。
P4103 代码
/*******************************
| Author: DE_aemmprty
| Remember:
* Read the question carefully!!!!!!
* If you don't make progress on a question within five minutes, it's very likely that you are going in the wrong direction.
* Don't rush to write code. Take your time.
* If Div.2D is not made, it indicates that you have been defrauded.
*******************************/
#include <bits/stdc++.h>
using namespace std;
template < typename T, typename...V > void chkMn(T &x, T y) { x = (x < y ? x : y); }
template < typename T, typename...V > void chkMx(T &x, T y) { x = (x < y ? y : x); }
long long read() {
char c = getchar();
long long x = 0, p = 1;
while ((c < '0' || c > '9') && c != '-') c = getchar();
if (c == '-') p = -1, c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * p;
}
const int N = 1e6 + 7;
struct Edge {
int v, w;
};
int n, q, k;
vector<int> to[N];
vector<Edge> re[N];
vector<int> S, T;
int d[N], dfn[N], c[N], tot;
int px[N][21], siz[N], f[N], mn[N], mx[N];
bool tag[N];
void dfs(int u, int fa, int dp) {
dfn[u] = ++ tot, c[tot] = fa;
d[u] = dp, f[u] = fa;
for (int v : to[u]) {
if (v == fa) continue;
dfs(v, u, dp + 1);
}
}
int cmp(int x, int y) {
return (dfn[x] < dfn[y] ? x : y);
}
void st_init() {
for (int i = 1; i <= n; i ++)
px[i][0] = c[i];
for (int j = 1; j <= 20; j ++)
for (int i = 1; i <= n - (1 << j) + 1; i ++)
px[i][j] = cmp(px[i][j - 1], px[i + (1 << (j - 1))][j - 1]);
}
int getLCA(int u, int v) {
if (u == v) return u; u = dfn[u], v = dfn[v];
if (u > v) swap(u, v); u ++;
int p = __lg(v - u + 1), q = (1 << p);
int ret = cmp(px[u][p], px[v - q + 1][p]);
// printf("%d, %d, ret = %d\n", px[dfn[u]][p], px[dfn[v] - q + 1][p], ret);
return ret;
}
int build(vector<int> &s) {
sort(s.begin(), s.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
vector<int> tmp; tmp.push_back(s[0]);
for (int i = 1; i < (int) s.size(); i ++) {
int c = getLCA(s[i - 1], s[i]);
tmp.push_back(s[i]), tmp.push_back(c);
}
sort(tmp.begin(), tmp.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
int m = unique(tmp.begin(), tmp.end()) - tmp.begin();
for (int i = 1; i < m; i ++) {
int c = getLCA(tmp[i - 1], tmp[i]);
re[c].push_back({tmp[i], d[tmp[i]] - d[c]});
re[tmp[i]].push_back({c, d[tmp[i]] - d[c]});
// printf("%d fa = %d\n", tmp[i], c);
}
s = tmp;
return tmp[0];
}
long long ans1;
int ans2, ans3;
void dfs2(int u, int fa) {
siz[u] = tag[u];
mn[u] = (tag[u] ? 0 : 2e9), mx[u] = (tag[u] ? 0 : -2e9);
for (auto tx : re[u]) {
int v = tx.v, w = tx.w;
if (v == fa) continue;
dfs2(v, u), siz[u] += siz[v];
ans1 += 1ll * siz[v] * w * (k - siz[v]);
chkMn(ans2, mn[u] + mn[v] + w);
chkMx(ans3, mx[u] + mx[v] + w);
mn[u] = min(mn[u], mn[v] + w);
mx[u] = max(mx[u], mx[v] + w);
}
}
void solve() {
n = read();
for (int i = 1, u, v; i < n; i ++) {
u = read(), v = read();
to[u].push_back(v);
to[v].push_back(u);
}
dfs(1, 0, 0);
st_init();
q = read();
while (q --) {
k = read(); S.clear();
for (int i = 1, x; i <= k; i ++)
x = read(), S.push_back(x), tag[x] = 1;
T = S; int rt = build(T);
ans1 = 0, ans2 = 2e9, ans3 = -2e9;
dfs2(rt, 0);
cout << ans1 << ' ' << ans2 << ' ' << ans3 << '\n';
for (int x : T) re[x].clear(), tag[x] = 0;
}
}
signed main() {
int t = 1;
while (t --) solve();
return 0;
}
CF613D Kingdom and its Cities
题目描述
与此同时，K 王国正在为国王女儿的婚礼做准备。然而，为了不在亲戚面前丢脸，国王必须先完成对王国的改革。由于国王迫不及待地想让女儿出嫁，改革必须尽快完成。
该王国目前由 \(n\) 个城市组成。城市之间通过 \(n-1\) 条双向道路连接，使得任意两个城市之间都可以互相到达。由于国王需要节省开支，所以任意两个城市之间只有一条路径。
改革的目的是什么？国家的重要部门需要分别迁移到不同的城市（我们称这些城市为“重要城市”）。然而，考虑到有蛮族入侵的高风险，必须谨慎进行。国王制定了多个计划，每个计划都描述了一组重要城市，现在他想知道哪个计划最优。
蛮族可以攻占一些非重要城市（重要城市肯定会有足够的保护），被攻占的城市将变得无法通行。具体来说，对于一个计划，其一个有趣的特性是：让所有重要城市都相互隔离（即从任何一个重要城市都无法到达其余重要城市）时，蛮族至少需要攻占多少个城市。
请帮助国王计算每个计划所需攻占的最少城市数。如果蛮族无论怎么攻占，都不能彻底隔离所有重要城市，请输出 \(-1\)。
显然，对于虚树上的一条边，在原树上只要被删除一条边，虚树上这条边也会断掉。
因此，设 \(f_{i, 0/1}\) 表示 \(i\) 的子树中，删了一些点之后，\(i\) 所在连通块内是否有关键点。这里，我们称 \(i\) 被删除时是 \(f_{i, 0}\)。
考虑 \(f_{u, 0/1}\) 如何转移。
-
如果 \(u\) 是非关键点，且我们删除了 \(u\)，那么就有 \(f_{u, 0} = 1 + \sum \min(f_{v, 0}, f_{v, 1})\)。
-
如果 \(u\) 是关键点，且 \(u\) 没被删除，那么就有 \(f_{u, 1} = \sum \min(f_{v, 0}, f_{v, 1} + 1)\)。
-
如果 \(u\) 是非关键点，且 \(u\) 没被删除，那么就有 \(f_{u, 0} = \sum \min(f_{v, 0}, f_{v, 1} + 1)\)，且 \(f_{u, 1} = f_{u, 0} - 1\) 当 \(f_{u, 0}\) 存在一个 \(f_{v, 1} + 1\) 的决策。
注意判断无解即可。
CF613D 代码
/*******************************
| Author: DE_aemmprty
| Remember:
* Read the question carefully!!!!!!
* If you don't make progress on a question within five minutes, it's very likely that you are going in the wrong direction.
* Don't rush to write code. Take your time.
* If Div.2D is not made, it indicates that you have been defrauded.
*******************************/
#include <bits/stdc++.h>
using namespace std;
template < typename T, typename...V > void chkMn(T &x, T y) { x = (x < y ? x : y); }
template < typename T, typename...V > void chkMx(T &x, T y) { x = (x < y ? y : x); }
long long read() {
char c = getchar();
long long x = 0, p = 1;
while ((c < '0' || c > '9') && c != '-') c = getchar();
if (c == '-') p = -1, c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * p;
}
const int N = 1e6 + 7;
struct Edge {
int v, w;
};
int n, q, k;
vector<int> to[N];
vector<Edge> re[N];
vector<int> S, T;
int d[N], dfn[N], c[N], tot;
int px[N][21], siz[N], f[N];
long long dp[N][2];
bool tag[N];
void dfs(int u, int fa, int dp) {
dfn[u] = ++ tot, c[tot] = fa;
d[u] = dp, f[u] = fa;
for (int v : to[u]) {
if (v == fa) continue;
dfs(v, u, dp + 1);
}
}
int cmp(int x, int y) {
return (dfn[x] < dfn[y] ? x : y);
}
void st_init() {
for (int i = 1; i <= n; i ++)
px[i][0] = c[i];
for (int j = 1; j <= 20; j ++)
for (int i = 1; i <= n - (1 << j) + 1; i ++)
px[i][j] = cmp(px[i][j - 1], px[i + (1 << (j - 1))][j - 1]);
}
int getLCA(int u, int v) {
if (u == v) return u; u = dfn[u], v = dfn[v];
if (u > v) swap(u, v); u ++;
int p = __lg(v - u + 1), q = (1 << p);
int ret = cmp(px[u][p], px[v - q + 1][p]);
// printf("%d, %d, ret = %d\n", px[dfn[u]][p], px[dfn[v] - q + 1][p], ret);
return ret;
}
int build(vector<int> &s) {
sort(s.begin(), s.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
vector<int> tmp; tmp.push_back(s[0]);
for (int i = 1; i < (int) s.size(); i ++) {
int c = getLCA(s[i - 1], s[i]);
tmp.push_back(s[i]), tmp.push_back(c);
}
sort(tmp.begin(), tmp.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
int m = unique(tmp.begin(), tmp.end()) - tmp.begin();
for (int i = 1; i < m; i ++) {
int c = getLCA(tmp[i - 1], tmp[i]);
re[c].push_back({tmp[i], d[tmp[i]] - d[c]});
re[tmp[i]].push_back({c, d[tmp[i]] - d[c]});
// printf("%d fa = %d\n", tmp[i], c);
}
s = tmp;
return tmp[0];
}
void dfs2(int u, int fa) {
siz[u] = tag[u];
dp[u][0] = dp[u][1] = 2e12;
long long ret1 = 0, ret2 = 0, ret3 = 2e12;
for (auto tx : re[u]) {
int v = tx.v, w = tx.w;
if (v == fa) continue;
dfs2(v, u), siz[u] += siz[v];
ret1 += min(dp[v][0], dp[v][1]);
ret2 += min(dp[v][0], (w > 1 ? dp[v][1] + 1 : (long long) 2e18));
chkMn(ret3, min(dp[v][0], dp[v][1]) - min(dp[v][0], (w > 1 ? dp[v][1] + 1 : (long long) 2e18)));
}
if (!tag[u]) chkMn(dp[u][0], ret1 + 1);
if (tag[u]) chkMn(dp[u][1], ret2);
if (!tag[u]) chkMn(dp[u][0], ret2);
if (!tag[u]) chkMn(dp[u][1], ret2 + ret3);
}
void solve() {
n = read();
for (int i = 1, u, v; i < n; i ++) {
u = read(), v = read();
to[u].push_back(v);
to[v].push_back(u);
}
dfs(1, 0, 0);
st_init();
q = read();
while (q --) {
k = read(); S.clear();
for (int i = 1, x; i <= k; i ++)
x = read(), S.push_back(x), tag[x] = 1;
T = S; int rt = build(T);
dfs2(rt, 0);
cout << (min(dp[rt][0], dp[rt][1]) >= 1e12 ? -1 : min(dp[rt][0], dp[rt][1])) << '\n';
for (int x : T) re[x].clear(), tag[x] = 0;
}
}
signed main() {
int t = 1;
while (t --) solve();
return 0;
}
P7737 庆典
题目描述
C 国是一个繁荣昌盛的国家，它由 $n$ 座城市和 $m$ 条有向道路组成，城市从 $1$ 到 $n$ 编号。如果从 $x$ 号城市出发，经过若干条道路后能到达 $y$ 号城市，那么我们称 $x$ 号城市可到达 $y$ 号城市，记作 $x\Rightarrow y$。C 国的道路有一个特点：对于三座城市 $x$，$y$，$z$，若 $x\Rightarrow z$ 且 $y\Rightarrow z$，那么有 $x\Rightarrow y$ 或 $y\Rightarrow x$。
再过一个月就是 C 国成立的千年纪念日，所以 C 国的人民正在筹备盛大的游行庆典。目前 C 国得知接下来会有 \(q\) 次游行计划，第 \(i\) 次游行希望从城市 \(s_i\) 出发，经过若干个城市后，在城市 \(t_i\) 结束，且在游行过程中，一个城市可以被经过多次。为了增加游行的乐趣，每次游行还会临时修建出 \(k\)（\(0 \le k \le 2\)）条有向道路专门供本次游行使用，即其它游行计划不能通过本次游行修建的道路。
现在 C 国想知道，每次游行计划可能会经过多少座城市。
注意：临时修建出的道路可以不满足 C 国道路原有的特点。
首先容易发现我们只关注连通性。因此，考虑删除一些边，只留下一些边使得点与点之间的可达关系仍然不变。
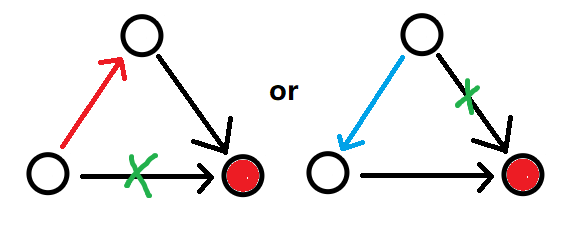
我们关注这个红点。假设这个红点的入度 \(\geq 2\)，那随便选两个点，这两个点之间一定有可达关系。如果我们只考虑连通性，显然有一条边可以被去除，这时候红点的入读会减去 \(1\)。
通过这种删边操作，我们可以把所有点的入读都变成 \(\geq 1\)。考虑缩点，由于缩点之后是一个 DAG，并且每个点的入读都 \(\geq 1\)，因此这一定是一颗树。
所以，我们对原图缩点后，这颗树的可达关系呈现出一棵树的形式。求出这棵树很简单，拓扑排序即可。
那么对于每个询问，将新增了有向边的点和 \(s, t\) 放到一起求出虚树，然后暴力跑出答案即可。
点击查看代码
/*******************************
| Author: DE_aemmprty
| Remember:
* Read the question carefully!!!!!!
* If you don't make progress on a question within five minutes, it's very likely that you are going in the wrong direction.
* Don't rush to write code. Take your time.
* If Div.2D is not made, it indicates that you have been defrauded.
*******************************/
#include <bits/stdc++.h>
using namespace std;
template < typename T, typename...V > void chkMn(T &x, T y) { x = (x < y ? x : y); }
template < typename T, typename...V > void chkMx(T &x, T y) { x = (x < y ? y : x); }
long long read() {
char c = getchar();
long long x = 0, p = 1;
while ((c < '0' || c > '9') && c != '-') c = getchar();
if (c == '-') p = -1, c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * p;
}
const int N = 1e6 + 7;
struct Node { int v, id; };
struct Edge { int v, w, id; };
struct Road { int u, v; };
vector<Node> wjc[N];
vector<Edge> re[N * 2], re2[N * 2];
vector<int> to[N * 2];
// Need: graph(vector<Node> wjc[N]) -> graph(vector<int> to[N * 2])
namespace SCC {
int __n__ = 0, dfn[N], low[N], bel[N], tot, col;
vector<int> scc[N];
stack<int> st;
void Tarjan(int u) {
low[u] = dfn[u] = ++ tot, st.push(u);
for (auto shx : wjc[u]) {
int v = shx.v;
if (!dfn[v]) {
Tarjan(v);
low[u] = min(low[u], low[v]);
} else if (!bel[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
col ++; int x;
do { x = st.top(); bel[x] = col; scc[col].push_back(x); st.pop(); } while (u != x);
}
}
void Build(int n) {
for (int i = 1; i <= n; i ++)
for (auto v : wjc[i])
if (bel[i] != bel[v.v])
to[bel[i]].push_back(bel[v.v]);
}
void outputSCC() {
cout << "==ECC==\n";
for (int i = 1; i <= col; i ++) {
for (int x : scc[i])
cout << x << ' ';
cout << '\n';
}
cout << "==end==\n";
}
void __init__() {
for (int i = 1; i <= __n__; i ++)
bel[i] = dfn[i] = low[i] = 0;
for (int i = 1; i <= __n__ + col; i ++) to[i].clear();
for (int i = 1; i <= col; i ++)
scc[i].clear();
tot = col = 0;
while (!st.empty())
st.pop();
}
void getSCC(int n) {
__init__(); __n__ = n;
for (int i = 1; i <= n; i ++)
if (!dfn[i]) Tarjan(i);
}
}
namespace topo {
int __n__, ind[N];
vector<int> tmp[N];
void __init__(int n) {
for (int i = 1; i <= __n__; i ++)
tmp[i].clear(), ind[i] = 0;
__n__ = n;
}
int topo() {
for (int i = 1; i <= __n__; i ++)
for (int v : to[i])
ind[v] ++;
vector<int> q;
for (int i = 1; i <= __n__; i ++)
if (!ind[i]) q.push_back(i);
for (int i = 0; i < __n__; i ++) {
int x = q[i];
for (int v : to[x]) {
ind[v] --;
if (!ind[v]) {
tmp[x].push_back(v);
q.push_back(v);
}
}
}
for (int i = 1; i <= __n__; i ++)
to[i] = tmp[i];
return q[0];
}
}
// Need: graph(vector<int> to[N]) -> graph(vector<Edge> re[N])
namespace VT {
int __n__, px[N][21], d[N], dfn[N], w[N], tot, etot;
bool imp[N];
void dfs(int u, int fa, int dp) {
w[u] = (int) SCC::scc[u].size(); dp += w[u];
dfn[u] = ++ tot, px[tot][0] = fa, d[u] = dp;
for (int v : to[u]) {
if (v == fa) continue;
dfs(v, u, dp);
}
}
int cmp(int x, int y) {
return (dfn[x] < dfn[y] ? x : y);
}
void st_init() {
for (int j = 1; j <= 20; j ++)
for (int i = 1; i <= __n__ - (1 << j) + 1; i ++)
px[i][j] = cmp(px[i][j - 1], px[i + (1 << (j - 1))][j - 1]);
}
int getLCA(int u, int v) {
if (u == v) return u; u = dfn[u], v = dfn[v];
if (u > v) swap(u, v); u ++;
int p = __lg(v - u + 1), q = (1 << p);
int ret = cmp(px[u][p], px[v - q + 1][p]);
return ret;
}
int Build(vector<int> &s) {
sort(s.begin(), s.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
for (int x : s) imp[x] = 1;
vector<int> tmp; tmp.push_back(s[0]);
for (int i = 1; i < (int) s.size(); i ++) {
int c = getLCA(s[i - 1], s[i]);
tmp.push_back(s[i]), tmp.push_back(c);
}
sort(tmp.begin(), tmp.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
int m = unique(tmp.begin(), tmp.end()) - tmp.begin();
for (int i = 1; i < m; i ++) {
int c = getLCA(tmp[i - 1], tmp[i]);
re[c].push_back({tmp[i], d[tmp[i]] - d[c] - w[tmp[i]], ++ etot});
re2[tmp[i]].push_back({c, d[tmp[i]] - d[c] - w[tmp[i]], etot});
}
s = tmp;
return s[0];
}
void clear(vector<int> s) {
etot = 0;
for (int i : s) {
re[i].clear();
re2[i].clear();
imp[i] = 0;
}
}
void __init__(int siz, int u) {
__n__ = siz, etot = tot = 0;
dfs(u, 0, 1);
st_init();
}
}
namespace mian {
int n, m, q, k;
vector<int> S, T;
Road p[7];
bool vis[N][2], evis[N][2];
void clear() {
for (int i = 1; i <= n; i ++)
wjc[i].clear();
}
void dfsS(int u) {
if (vis[u][0]) return ;
vis[u][0] = 1;
for (auto v : re[u]) {
dfsS(v.v);
evis[v.id][0] = 1;
}
}
void dfsT(int u, int &res) {
if (vis[u][1]) return ;
vis[u][1] = 1; res += vis[u][0] * ((int) SCC::scc[u].size());
for (auto v : re2[u]) {
dfsT(v.v, res);
res += (evis[v.id][1] == 0 && evis[v.id][0] == 1) * v.w;
evis[v.id][1] = 1;
}
}
void solve() {
n = read(), m = read(), q = read(), k = read();
for (int i = 1, u, v; i <= m; i ++) {
u = read(), v = read();
wjc[u].push_back({v, i});
}
SCC::getSCC(n), SCC::Build(n); int m = SCC::col;
topo::__init__(m);
VT::__init__(m, topo::topo());
while (q --) {
int s = read(), t = read();
S.clear(), S.push_back(SCC::bel[s]), S.push_back(SCC::bel[t]);
for (int i = 1; i <= k; i ++) {
p[i].u = read(), p[i].v = read();
S.push_back(SCC::bel[p[i].u]), S.push_back(SCC::bel[p[i].v]);
}
VT::Build((T = S));
for (int i = 1; i <= k; i ++) {
re[SCC::bel[p[i].u]].push_back({SCC::bel[p[i].v], 0, ++ VT::etot});
re2[SCC::bel[p[i].v]].push_back({SCC::bel[p[i].u], 0, VT::etot});
}
int res = 0;
dfsS(SCC::bel[s]), dfsT(SCC::bel[t], res);
cout << res << '\n';
for (int x : T) vis[x][0] = vis[x][1] = 0;
for (int i = 1; i <= VT::etot; i ++) evis[i][0] = evis[i][1] = 0;
VT::clear(T);
}
clear();
}
}
signed main() {
int t = 1;
while (t --)
mian::solve();
return 0;
}
P4606 战略游戏
题目描述
省选临近，放飞自我的小 Q 无心刷题，于是怂恿小 C 和他一起颓废，玩起了一款战略游戏。
这款战略游戏的地图由 \(n\) 个城市以及 \(m\) 条连接这些城市的双向道路构成，并且从任意一个城市出发总能沿着道路走到任意其他城市。
现在小 C 已经占领了其中至少两个城市，小 Q 可以摧毁一个小 C 没占领的城市，同时摧毁所有连接这个城市的道路。只要在摧毁这个城市之后能够找到某两个小 C 占领的城市 \(u\) 和 \(v\)，使得从 \(u\) 出发沿着道路无论如何都不能走到 \(v\)，那么小 Q 就能赢下这一局游戏。
小 Q 和小 C 一共进行了 \(q\) 局游戏，每一局游戏会给出小 C 占领的城市集合 \(S\)，你需要帮小 Q 数出有多少个城市在他摧毁之后能够让他赢下这一局游戏。
缩点，建出圆方树，在圆方树上跑虚树，计算边权上的割点个数 + 非叶子非关键点的割点个数即可。
点击查看代码
/*******************************
| Author: DE_aemmprty
| Remember:
* Read the question carefully!!!!!!
* If you don't make progress on a question within five minutes, it's very likely that you are going in the wrong direction.
* Don't rush to write code. Take your time.
* If Div.2D is not made, it indicates that you have been defrauded.
*******************************/
#include <bits/stdc++.h>
using namespace std;
template < typename T, typename...V > void chkMn(T &x, T y) { x = (x < y ? x : y); }
template < typename T, typename...V > void chkMx(T &x, T y) { x = (x < y ? y : x); }
long long read() {
char c = getchar();
long long x = 0, p = 1;
while ((c < '0' || c > '9') && c != '-') c = getchar();
if (c == '-') p = -1, c = getchar();
while (c >= '0' && c <= '9')
x = (x << 1) + (x << 3) + (c ^ 48), c = getchar();
return x * p;
}
const int N = 1e6 + 7;
struct Node { int v, id; };
struct Edge { int v, w; };
vector<Node> wjc[N];
vector<Edge> re[N * 2];
vector<int> to[N * 2];
// Need: graph(vector<Node> wjc[N]) -> graph(vector<int> to[N * 2])
namespace VCC {
int __n__ = 0, dfn[N], low[N], cnt[N], tot, col;
bool cut[N];
vector<int> vcc[N];
stack<int> st;
void Tarjan(int u, int eid) {
low[u] = dfn[u] = ++ tot, st.push(u);
int son = 0;
for (auto shx : wjc[u]) {
int v = shx.v, id = shx.id;
if (!dfn[v]) {
son ++, Tarjan(v, id);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
col ++; int tmp;
do { tmp = st.top(); vcc[col].push_back(tmp); st.pop(); } while (tmp != v);
vcc[col].push_back(u);
}
} else if (id != eid) {
low[u] = min(low[u], dfn[v]);
}
}
if (!eid && !son) vcc[++ col].push_back(u);
}
void Build(int n) {
for (int i = 1; i <= col; i ++) {
++ n;
for (int x : vcc[i]) {
to[x].push_back(n);
to[n].push_back(x);
cnt[x] ++;
}
}
for (int i = 1; i <= n; i ++)
if (cnt[i] > 1) cut[i] = 1;
}
void outputVCC() {
cout << "==VCC==\n";
for (int i = 1; i <= col; i ++) {
for (int x : vcc[i])
cout << x << ' ';
cout << '\n';
}
cout << "==end==\n";
}
void __init__() {
// printf("__n__ = %d\n", __n__);
for (int i = 1; i <= __n__; i ++)
cnt[i] = cut[i] = dfn[i] = low[i] = 0;
for (int i = 1; i <= __n__ + col; i ++) to[i].clear();
for (int i = 1; i <= col; i ++)
vcc[i].clear();
tot = col = 0;
while (!st.empty())
st.pop();
}
void getVCC(int n) {
__init__(); __n__ = n;
for (int i = 1; i <= n; i ++)
if (!dfn[i]) Tarjan(i, 0);
}
}
// Need: graph(vector<int> to[N]) -> graph(vector<Edge> re[N])
namespace VT {
int __n__, px[N][21], d[N], dfn[N], tot;
bool imp[N];
void dfs(int u, int fa, int dp) {
dfn[u] = ++ tot, px[tot][0] = fa, d[u] = dp;
for (int v : to[u]) {
if (v == fa) continue;
dfs(v, u, dp + VCC::cut[v]);
}
}
int cmp(int x, int y) {
return (dfn[x] < dfn[y] ? x : y);
}
void st_init() {
for (int j = 1; j <= 20; j ++)
for (int i = 1; i <= __n__ - (1 << j) + 1; i ++)
px[i][j] = cmp(px[i][j - 1], px[i + (1 << (j - 1))][j - 1]);
}
int getLCA(int u, int v) {
if (u == v) return u; u = dfn[u], v = dfn[v];
if (u > v) swap(u, v); u ++;
int p = __lg(v - u + 1), q = (1 << p);
int ret = cmp(px[u][p], px[v - q + 1][p]);
return ret;
}
int Build(vector<int> &s) {
sort(s.begin(), s.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
for (int x : s) imp[x] = 1;
vector<int> tmp; tmp.push_back(s[0]);
for (int i = 1; i < (int) s.size(); i ++) {
int c = getLCA(s[i - 1], s[i]);
tmp.push_back(s[i]), tmp.push_back(c);
}
sort(tmp.begin(), tmp.end(), [&](int x, int y) {
return dfn[x] < dfn[y];
});
int m = unique(tmp.begin(), tmp.end()) - tmp.begin();
for (int i = 1; i < m; i ++) {
int c = getLCA(tmp[i - 1], tmp[i]);
re[c].push_back({tmp[i], d[tmp[i]] - d[c] - VCC::cut[tmp[i]]});
re[tmp[i]].push_back({c, d[tmp[i]] - d[c] - VCC::cut[tmp[i]]});
}
s = tmp;
return s[0];
}
void clear(vector<int> s) {
for (int i : s) {
re[i].clear();
imp[i] = 0;
}
}
void __init__(int siz, int u) {
__n__ = siz, tot = 0;
dfs(u, 0, 1);
st_init();
}
}
namespace mian {
int n, m, q, k;
vector<int> S, T;
void clear() {
for (int i = 1; i <= n; i ++)
wjc[i].clear();
}
void dfs2(int u, int fa, int &ans) {
bool lf = 1;
for (Edge wjc : re[u]) {
int v = wjc.v, w = wjc.w;
if (v == fa) continue;
dfs2(v, u, ans);
ans += w, lf = 0;
}
if (!lf) ans += (VCC::cut[u] && !VT::imp[u]);
}
void solve() {
n = read(), m = read();
for (int i = 1, u, v; i <= m; i ++) {
u = read(), v = read();
wjc[u].push_back({v, i});
wjc[v].push_back({u, i});
}
VCC::getVCC(n), VCC::Build(n);
int m = n + VCC::col;
VT::__init__(m, 1);
q = read();
while (q --) {
k = read(); S.clear();
for (int i = 1, x; i <= k; i ++)
x = read(), S.push_back(x);
int rt = VT::Build((T = S)), ans = 0;
dfs2(rt, 0, ans);
cout << ans << '\n';
VT::clear(T);
}
clear();
}
}
signed main() {
int t = read();
while (t --)
mian::solve();
return 0;
}
浙公网安备 33010602011771号