骗我呢题解 / 反射容斥笔记

\(\mathbf{Part. 1}\)

从右往左考虑肯定没啥前途，我们考虑从上往下扫行。对于每一行，它上面的元素肯定都是单调递增的，又知道元素的值域在 \(0\) 到 \(m\)，而一行总共有 \(m\) 个数，因此每行可以被表示为 \(0\) 到 \(m\) 失去一个数后按顺序排好。因此，我们可以用一个 \(0 \leq x \leq m\) 的数来表示一行。

我们设 \(f_{i, j}\) 表示前 \(i\) 行，第 \(i\) 行失去了 \(j\) 的方案数。那么，考虑相邻两行如何转移。

首先，假设我们要从 \(i - 1\) 向 \(i\) 转移，而 \(i - 1\) 失去的是 \(x\)。分两部分：

• 对于第 \(i - 1\) 行的 \(x + 1\) 到 \(m\)，转移到 \(i\) 行后肯定是 \(x + 2\) 到 \(m\)
• 对于 \(0\) 到 \(x - 1\)，我们可以让消失的数从 \(0\) 取到 \((x + 2) - 1 = x + 1\)

上面结合具体实例理解。

假设 \(i\) 失去了 \(x\)，\(i - 1\) 失去了 \(y\)，有 \(x \leq y - 1\)，因此 \(f_{i, j} = \sum_{k = 1}^{j + 1} f_{i - 1, k} = f_{i, j - 1} + f_{i - 1, j + 1}\)。

这里将求和转化为两个数相加十分关键。

我们观察这个 DP 式子，画出转移的图：

可以看到，有两种移动方式：向右或者向左上。不妨将这个东西转化为我们更熟悉的网格图，向右和向上。如图。

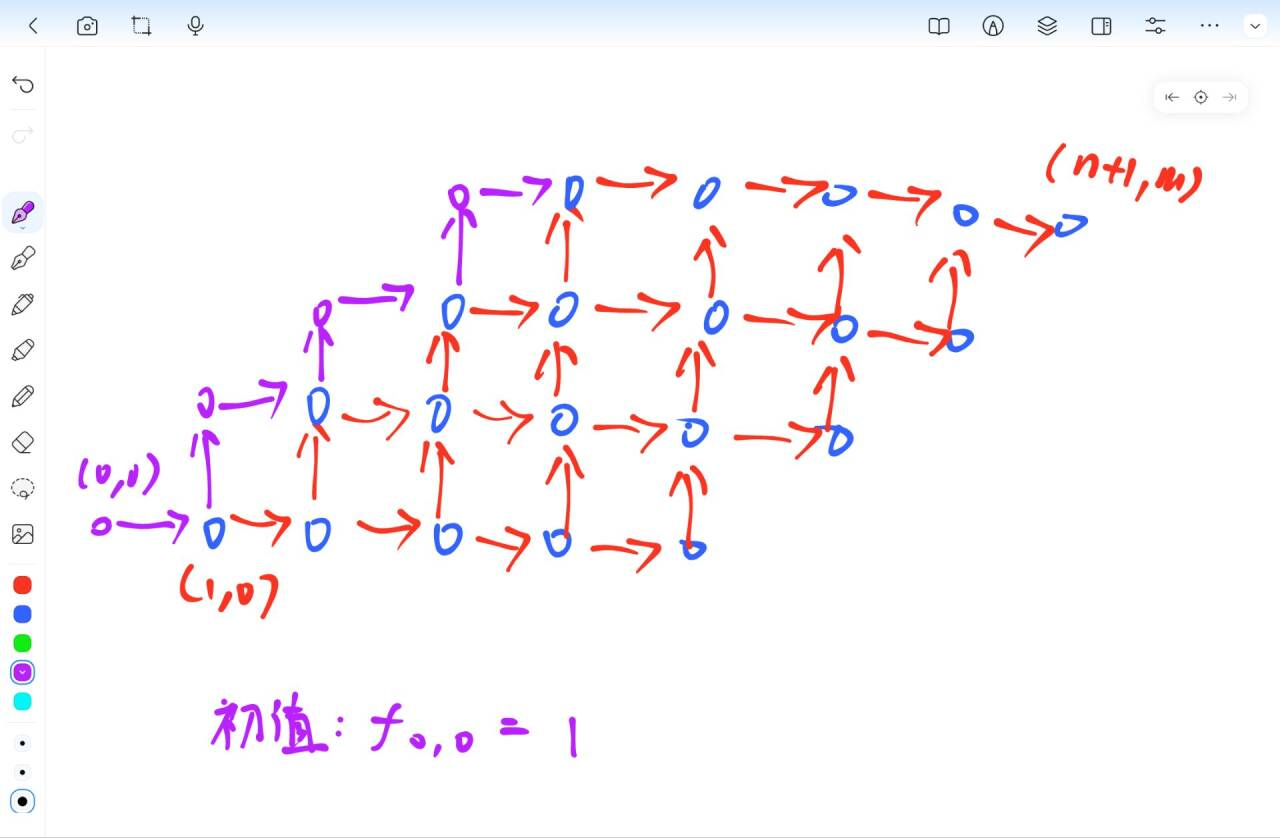
紫色是处理 \(f_{i, 0} = f_{i - 1, 0}\) 时的特殊转移。

那么，这个 DP 的式子实际上就等价于只经过图中的这些点和边，从 \((0, 0)\) 到 \((n + 1, m)\) 的方案数。

而这些边点的限制就相当于我们只能向右 / 向上走，不经过两边的斜率为 \(1\) 的斜线。

对于做括号序列比较多的同学来说，这个就比较经典了。

\(\mathbf{Part. 2}\)

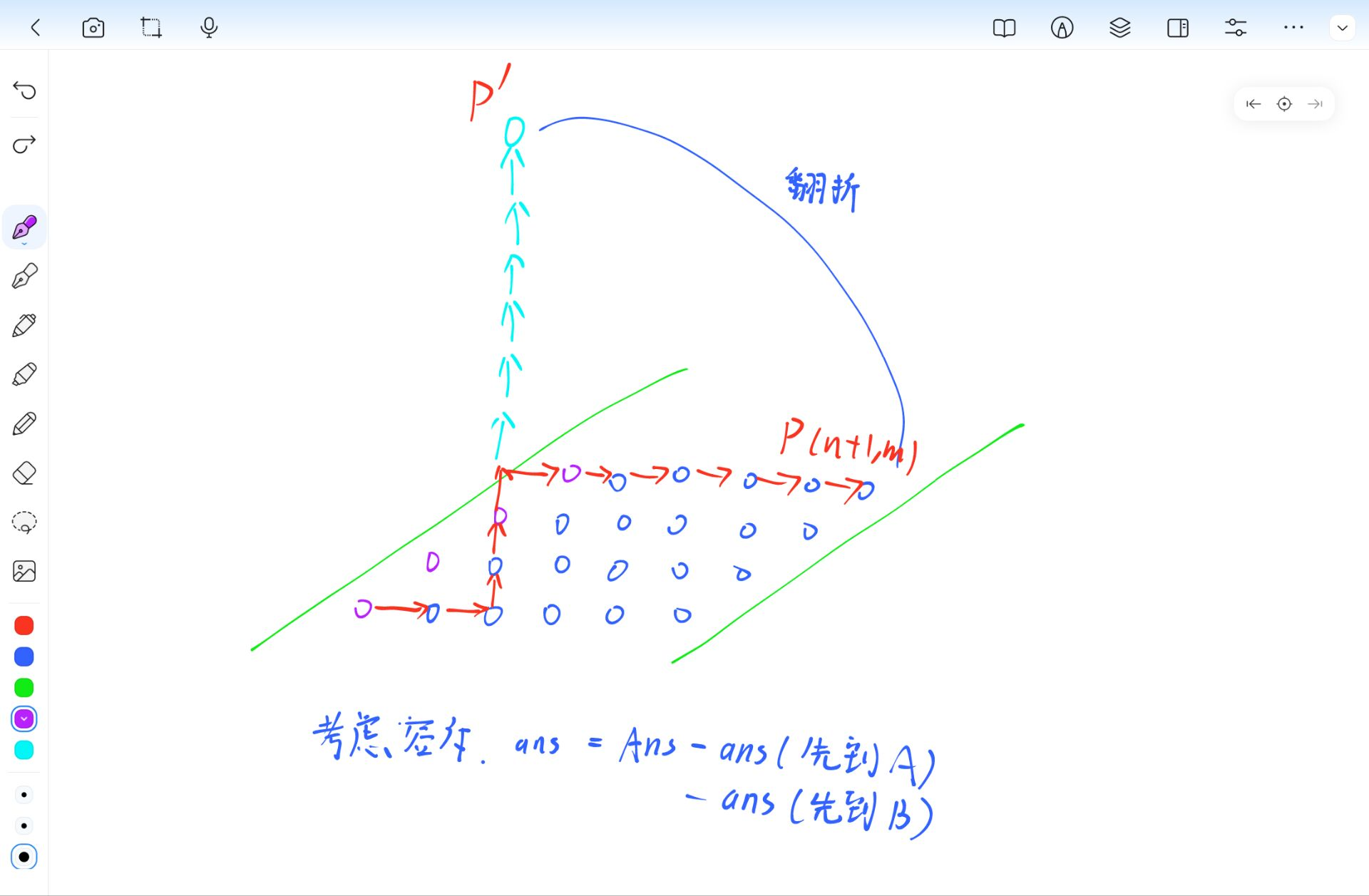
如上图，我们假设左边的斜线为 \(A\)，右边的为 \(B\)，那么先容斥， 答案转化为 \(\text{ALL} - \text{先碰到到 A 的路径个数} - \text{先碰到到 B 的路径个数}\)。其中 \(\text{ALL}\) 表示不考虑斜线的限制，合法路径个数。

但是“先碰到”这个不太好算，所以我们可以尝试把“先”去掉，只要这个路径碰到就行了。这启发我们容斥。

为了方便后面的描述，我们先给路径定义一个字符串。我们按时间的先后顺序，依次记录该路径与哪条直线产生交点，就可以得到一个形如 \(\texttt{AAABBAABBBB}\) 的字符串。然后，我们可以把相邻的字符压起来，前面的例子就是 \(\texttt{ABAB}\)。

Q1. 为什么可以这样缩

A1.

回顾 $\mathbf{Part. 3}$ 中我们对“经过 A”的路径个数是怎么计算的。容易发现，如果这条路径连续的经过同一条直线，我们实际上只是取经过直线的第一个交点进行翻折，而后面的交点不用在意。我们在计数的过程中，只关注在这段连续时间，该路径是不是只经过了 A，而不关注经过了多少次，因此可以压起来。

我们定义 \(f(t)\) 表示对应的字符串以 \(t\) 为子序列的路径个数，其中 \(f(\texttt{AB})\) 就表示经过了 \(\texttt{A}, \texttt{B}\) 的路径个数，\(f(\texttt{BAB})\) 就表示分别经过了 \(\texttt{B},\texttt{A},\texttt{B}\) 的路径个数。

我们再定义 \(g(t)\) 表示对应的字符串以 \(t\) 为前缀的路径个数，其中 \(g(\texttt{A})\) 就表示先碰到 \(\texttt{A}\) 的路径个数，\(g(\texttt{BAB})\) 就表示先分别碰到 \(\texttt{B},\texttt{A},\texttt{B}\) 的路径个数。

明确目标，我们想要计算先碰到 \(\texttt{A}\) 或 \(\texttt{B}\) 的路径个数，也就是 \(g(\texttt{A}) + g(\texttt{B})\)

考虑 \(f(\texttt{A}) + f(\texttt{B})\) 与 \(g(\texttt{A}) + g(\texttt{B})\) 相比的差异。如果一条路径是先碰到 \(\texttt{AB}\) 或者 \(\texttt{BA}\)，那么这种路径在 \(f(\texttt{A}) + f(\texttt{B})\) 中会被算两次，而在 \(g(\texttt{A}) + g(\texttt{B})\) 中只会被算一次，需要减去一。

因此，有 \(g(\texttt{A}) + g(\texttt{B}) = f(\texttt{A}) + f(\texttt{B}) - (g(\texttt{AB}) + g(\texttt{BA}))\)，而后面这个 \(g(\texttt{AB}) + g(\texttt{BA})\) 可以继续刚才的容斥。

递归下去能得到 \(g(\texttt{A}) + g(\texttt{B}) = f(\texttt{A}) + f(\texttt{B}) - f(\texttt{AB}) - f(\texttt{BA}) + f(\texttt{ABA}) - f(\texttt{BAB}) - \cdots\)

只要能算出来 \(f\)，答案就是 \(\text{ALL} - (f(\texttt{A}) + f(\texttt{B}) - f(\texttt{AB}) - f(\texttt{BA}) + f(\texttt{ABA}) - f(\texttt{BAB}) - \cdots)\)。

这就是反射容斥的核心部分。

\(\mathbf{Part. 3}\)

我们以 \(f(\texttt{AB})\) 和下图的这个路径为例，考虑如何计算 \(f\)。

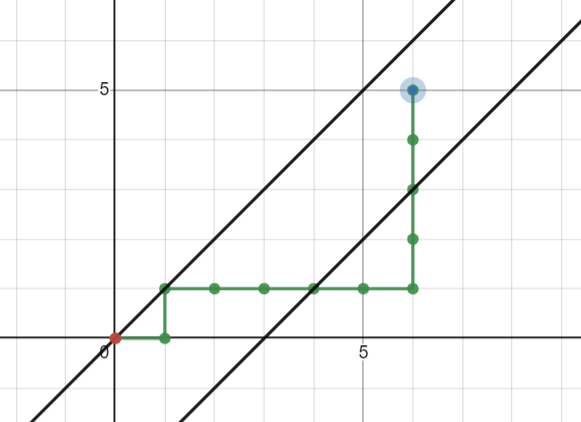
这是初始的路径，设上面的对角线是 \(A\)，下面的是 \(B\)。我们先将这个路径与 \(A\) 做一遍 \(\mathbf{Part. 3}\) 的翻转（同时，把 \(B\) 也对称过去），然后再将新的路径对新的 \(B\) 做一遍翻转。如下：

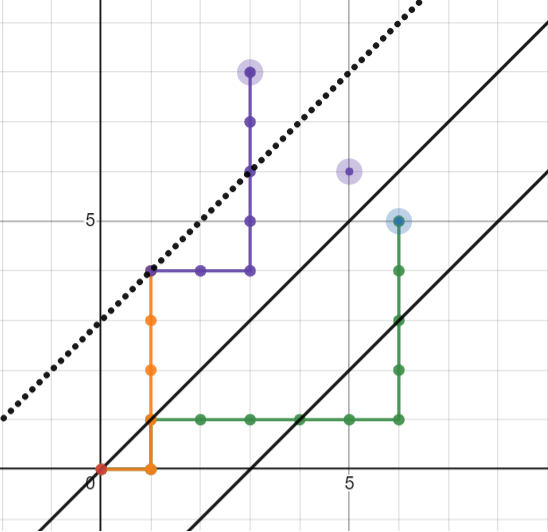
设终点为 \(P\)。第一次关于 \(y=x+b\) 对称，第二次关于 \(y=x+2b−c\)（也就是 \(y = x + b\) 关于 \(y = x + c\) 对称的结果）对称。假设对称完之后的终点在 \(P'\)

我们应该可以发现，从原点到 \(P'\) 的路径一一对应以 \(\texttt{AB}\) 为子序列，以 \(P\) 为终点的路径，因此只需要计算 \((0, 0)\) 到 \(P'(a, b)\) 的路径个数。

我们可以向左走 \(a\) 次，向上走 \(b\) 次，方案数为 \(\binom{a+b}{a}\)，表示从每次行动中选择 \(a\) 次向左走，剩余的向上走。

我们考虑更朴素的情况，设 \(F(S)\) 条路径对应的字符串是 \(S\)：

• 按顺序遍历字符。
• 如果是 \(A\)：\(P\) 和 \(y=x+c\) 都关于 \(y=x+b\) 对称。
• 如果是 \(B\)：\(P\) 和 \(y=x+b\) 都关于 \(y=x+c\) 对称。
• 最后得到的 \(P\) 到 \((0,0)\) 的路径数就是 \(F(S)\)。假设 \(P(a, b)\)，那么就有 \(F(S) = \binom{a + b}{b}\)。
• 如果 \(P\) 的横坐标或纵坐标小于 \(0\)，就舍去。

现在，结合 \(\mathbf{Part. 4}\) 的答案式，我们就可以解出此题。

\(\mathbf{Part.} +\infty\)

Q2. 这个容斥有点怪，它的容斥结构大概长什么样子？

A2.

关注 $\mathbf{Part. 4}$ 中 $g(A) + g(B)$ 的容斥过程，能发现这个容斥结构大概是 $|A| + |B| - |A \bigcap B|$，其中我们会对 $|A \bigcap B|$ 再进行一次容斥，变成 $|A| + |B| - |A'| - |B'| + |A' \bigcap B'|$，然后不断递归容斥下去。 因此，反射容斥实际上是一个容斥套容斥的结构，这比较特殊。

Q3. 为什么有人将这个容斥称为“前缀容斥”？

A3.

$f(t)$ 是子序列，$g(t)$ 是前缀，因为 $g(t)$ 也就是前缀不好算，所以我们通过容斥，将它转换成了与子序列相关的 $f(t)$。因此最终的结果式子中不带有 $g$ 函数。我们将前缀转化成了子序列，所以可以叫前缀容斥。