秋季记录

P10675 【MX-S1-T4】先见之明

原题

对于一次询问，考虑有哪些可能的解。首先是一些特殊的答案：\(ans=k,2^{p_1 + 1},2^{pre_{p_1 + 1}}\)，其中 \(pre_i\) 为 最小的 \(a_j\) 使得 \(a_j \ge i\)，这些都是可以快速判断的，先不考虑。

再就是答案肯定是 \(k\) 的一段前缀 \(+2^j\)，其中 \(j\notin k\)。设答案取了 \(2^{p_1} \sim 2^{p_i}\) 和 \(2^j (p_i > j > p_{i+1})\)，考虑这个 \(j\) 的取值可能是哪些。

• 如果这个 \(2^j\) 是用一些 \(\le 2^{p_{i+1}}\) 的 \(a\) 凑成的，那么肯定经过了这些 \(a\) 先加到 \(2^{p_{i+1}+1}\) 再不断进位到 \(2^j\)，既然中间都存在到一个更小值的过程，那把 \(j\) 换成 \(p_{i+1} + 1\) 肯定更优，所以一种可能的取值是 \(2^{p_{i+1} + 1}\)。

• 如果 \(2^j\) 用了 \(> 2^{p_{i+1}}\) 的 \(a\) 凑，那么这些 \(a\) 肯定不会 \(\le 2^{p_{i+1}}\)，理由同上。那么肯定只用一个 \(a\) 最优，且这个 \(a\) 肯定是出现在 \([p_{i+1} + 1,p_{i} - 1]\) 中最小的那个，证明和上面类似：如果取的不是最小那个，那么这个最小的用途肯定是去凑 \(\ge 2^{p_i}\) 的数了，中间肯定有个过程是变成了 \(2^j\)，那把这个 \(2^j\) 用一开始就存在的这个 \(2^j\) 替换掉肯定更优。

所以只会存在最多 \(2m\) 种取值，设取值为 \(j\) 的答案为 \(ans_j\)，容易发现 \(ans\) 是单调递增的。

考虑判定一个数 $x 能否被凑出来：

• 如果 \(x=2^t\)，那么只考虑 \(\le t\) 的 \(a_i\)，条件就是 \(\sum 2^{a_i} \ge x\)。

• 如果 \(x=\sum\limits_{i=1}^k 2^{b_i}(b_i < b_{i+1})\)，那么条件就是 \(\forall i,\sum\limits_{j\le i} 2^{b_j} \le \sum\limits_{a_j \le b_i} 2^{a_j}\)，容易归纳证明。

把这个条件放到 \(ans\) 上去看，对于一个 \(2^{p_i}\)，右边的 \(\sum\limits_{a_j \le p_i} 2^{a_j}\) 已经知道了，又因为 \(ans\) 是单调的，所以如果处理出一个 \(pos_i\) 表示最大的 \(ans_j\) 使得 \(ans_j\) 的 \(i\) 后面位置的和 \(\le \sum\limits_{a_j \le p_i} 2^{a_j}\)，那么判断 \(ans\) 只需要对 \(pos_{i}\) 维护前缀 \(\min\) 再额外判断一下 \(j\) 即可。

考虑咋处理这个 \(pos\)，先预处理一个 \(f_i,g_i\) 表示把 \(\le i\) 的 \(a\) 加起来（不进位到 \(i+1\)）得到的第 \(i\) 位的值和下一个 \(1\) 的位置。那么如果 \(f_{p_i} = 0\)，\(pos_i\) 就没救了，否则如果 \(>1\) 那么对于所有后缀都合法，令 \(pos_i=p_i\)，\(=1\) 可以讨论 \(g_i\) 的值通过 \(pos_{i+1}\) 递推得到。

复杂度就是预处理 \(\Theta(n+V)\)，每次询问 \(\Theta(m)\)，总复杂度就是 \(\Theta(n+V+\sum m)\)。

qoj9729 Dividing Sequence

原题

考虑 check 一个答案，可以考虑设 \(f_{i,j}\) 为前缀 \(i\) 中 \(C\) 字符串取了 \(j\) 个最小的 \(B\)，转移是简单的，那么只要 \(f_{n,|C|} \le C\)。

考虑每次在答案后面加一个字符，判断新的答案能否作为答案的一个前缀，那么此时 \(j<|C|\) 的状态可以舍去了，只需要保留 \(f_i\) 为前缀 \(i\) 取完 \(C\) 后剩下最小的 \(B\)，转移可以通过 \(f_i \to f'_{i+1}\) 或 \(f'_i \to f'_{i+1}\)，但是现在依旧是字符串比较，不优秀。

容易发现，比较难处理的 \(f_i\) 的情况是 \(C\) 是 \(f_i\) 的的前缀，但是可以证明，这种情况总是不优的。即存在一种调整方式，使得最后每个前缀（不计 \(A\) 已经比 \(B\) 小的时候）存在一种划分方式使得 \(B\) 在这个前缀中为 \(C\) 在这个前缀中的一个前缀。

• 证明：假设 \(1 \sim i - 1\) 都是 \(B\) 为 \(C\) 的一个前缀，到了 \(i\) 的时候 \(B\) 比 \(C\) 多了一个 \(x\)，考虑此时 \(C\) 的后一个字符 \(y\)。
  • 如果 \(x<y\)，那么 \(B\) 删掉 \(x\) 后面的东西，令 \(C\) 取完 \(y\) 之后的后缀肯定不劣。
  • 否则由于最后 \(B\le C\)，最终形态肯定如下图所示。先交换 \(i\) 位置之后的 \(B,C\)，如果交换前 \(B\) 结束位置在 \(C\) 之前，那么直接把 \(C\) 取完接下来的东西，\(B\) 变成一个前缀就行。不然从第一个不等的位置后往前交换调整。此时将短的位置看成 \(1\)，长的位置看成 \(0\)（如下图第一行为 \(0\)，第二行为 \(1\)），每次把最后一个 \(1\) 移上去，最后一个 \(0\) 移下来，如果第一行存在逆序对就继续调整，否则可以结束调整。由于长度总和相等，所以肯定可以结束调整。
    

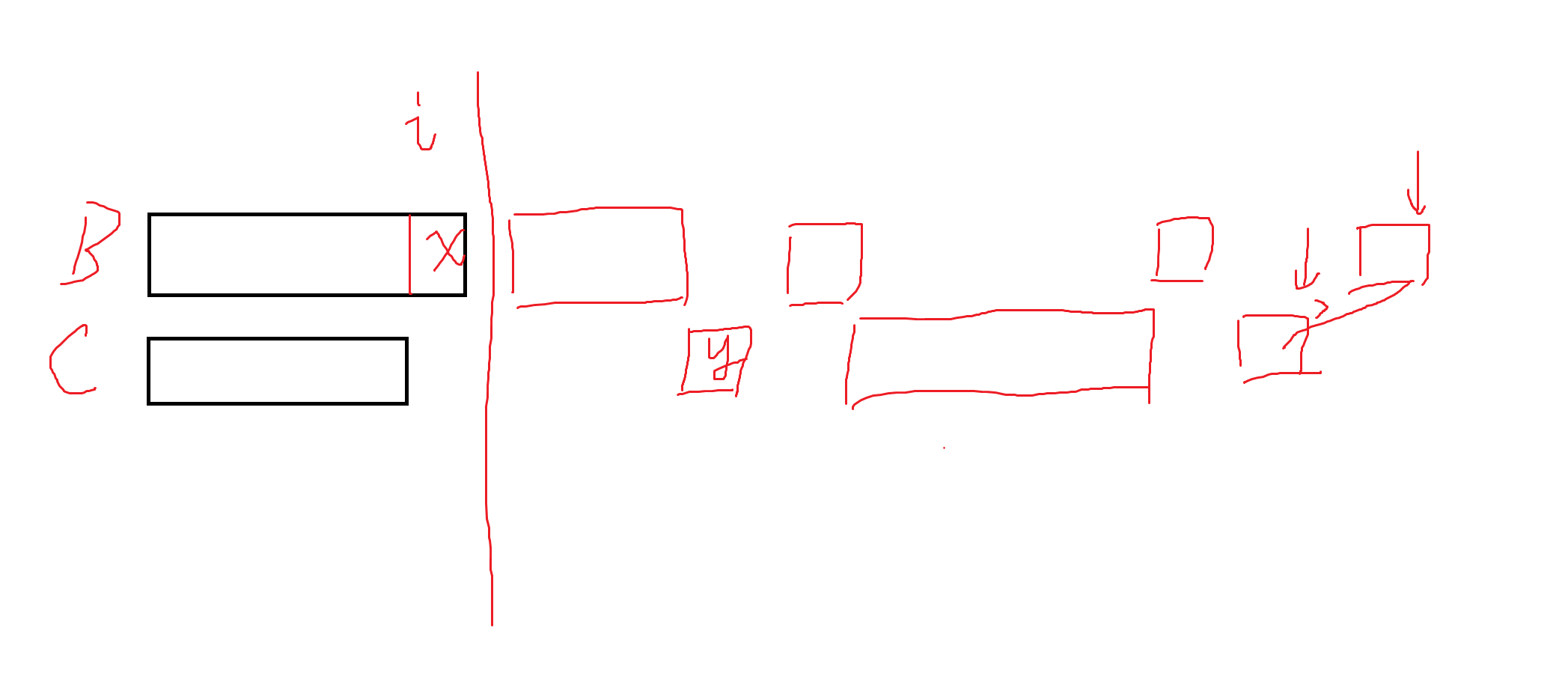
所以此时可以简化状态为 \(f_i\) 表示 \(B\) 取了 \(C\) 的前缀 \(i\) 是否合法，设 \(|C|=j\)，只需要取最小的合法 \(a_{i+j+1}\) 出来拓展就行，或者判断存在 \(a_{i+j+1}<C_{i+1}\) 就可以结束了。

CF2152 H2. Victorious Coloring (Hard Version)

原题

先考虑已知 \(x_i\) 怎么求 \(f(x_i)\)。设 \(a_u\) 为 \(u\) 头上的边，朴素的想法是直接 dp，\(dp_u = a_u + \sum\limits_v \min(dp_v - a_v, a_v)\)，然后对 \(l\) 取 \(\max\)，但是这个做法无法优化，故舍去。

先对原图找一点性质：对于最小的连通块，不存在一条内部到外部的边 \(w_i\) 比内部任意一条边的 \(w_j\) 大，否则可以让内部那条 \(w_j < w_i\) 的 \(j\) 作为内部到外部的边。所以从大往小加边，那么就只有每次加完边的连通块和一开始的孤点可能成为 \(f(x_i)\)。

考虑求答案，设 \(sum(S)\) 为联通块 \(S\) 的内部到外部边权和，\(ans_S\) 为 \(S\) 内部的 \(x\) 之和，显然要有 \(\forall S,ans(S) \ge l - sum(S)\)。

容易发现，上面的连通块可以通过 kruskal 重构树来表示，每个连通块就是一个子树，那么就有 \(ans_u = \max(ans_{ls_u} + ans_{rs_u}, l - sum(u))\)。

考虑直接维护 \(ans_u(l)\) 为关于 \(l\) 的一个函数。

• 对于叶子节点，\(ans_u\) 为一段 \(0\) 后加上一条斜率为 \(1\) 的直线，显然是凸的。

• 对于非叶子节点，\(ans_u\) 可以表示为两个凸函数之和和一个凸函数取 max，还是凸的。

用 slope trick 维护这个凸函数，合并两个子树的时候直接把两个堆 merge，取 max 的时候只用看最小的若干个点被一条斜率为 \(1\) 的直线弹掉即可，每次只会加 \(O(1)\) 个点。

所以复杂度为 \(O(n\log^2 n+q\log n)\) 或 \(O((n+q)\log n)\)，取决于是否使用可并堆。

qoj14432 Cyclic Topsort

原题

即除一个点的拓扑序（碰到环之前的）最长。先把本来合法的点删掉，设 \(s_u\) 为删掉 \(u\) 能合法的点集。考虑若 \(w \in s_u \land w\in s_v(u\neq v)\)，那么 \(u,v\) 要满足 \(s_u \subseteq s_v \lor s_v \subseteq s_u\)。证明是显然存在一条 \(u \to w\) 和 \(v \to w\) 的路径，若删 \(u\) 能使 \(w\) 合法，那么 \(v \to w\) 这条路径肯定是拓扑序小于 \(w\) 的且必须得合法，所以 \(v\) 此时也会合法。所以就有 \(\forall i \neq j, s_i \cap s_j = \empty \lor s_i \subseteq s_j \lor s_j \subseteq s_i\)，包含关系是一棵树（或森林）。

那么每次删一个点的时候，若这个点在之前的某个 \(s_v\) 中就可以跳过了，因为显然比它小。否则就暴力跑一遍，跑的时候可以用并查集维护每个已经访问过的连通块，遇到访问过的就直接返回这个集合大小。

或者可以随机排列后暴力跑，每次是 \(O(siz)\) 的，那么对于每个点访问次数是 \(E(len_{rt \to u})=O(\log n)\)。

复杂度为 \(O(n)\) 或 \(O(n\log n)\)。

P14135 【MX-X22-T6】「TPOI-4F」Miserable EXperience

原题

把子树操作放到最后来做，且子树操作合法当且仅当 \(\forall i,a_i \ge a_{fa_i}\)。

先差分一下，令 \(c_i = a_i - a_{fa_i}\)，那么就是要让 \(\forall i,c_i \ge 0\)，答案就是 \(\sum c_i\)。一次行操作就是将第 \(i\) 行的 \(c\) 减 \(1\)，\(i+1\) 行的 \(c\) 加 \(1\)，代价变化 \(cnt_{i+1} - cnt_{i} + 1\)。所以每行只和点个数 \(cnt_i\) 和 \(c\) 的最小值 \(p_i\) 有关。

先考虑 \(p_i \ge 0\) 的情况，考虑把操作 \(i,i+1,\ldots j\) 变为操作 \(i,j\)，代价为 \(cnt_j - cnt_i + j - i\)，设 \(b_i = cnt_i + i\)，即为 \(b_j - b_i\)。这样处理后就不存在形如 \((i,j),(j,k)\) 这样的重合操作了，所以每个点要么是只出，要么只进，对于只出的点，要求操作的次数 \(\le p_i\)（否则就小于 \(0\) 了）。贪心地，把每个点按 \(b_i\) 从小到大排序，每次取出最小的 \(b_i\) 把前面没匹配的都和它匹配即可（也即每个点向其后缀最小值匹配）。

对于存在 \(p_i < 0\) 的情况，可以先任意操作若干次将 \(p_i\) 都变成非负数再继续调整，只要调整能最优，那么肯定可以到达最优答案。

考虑优化，由于只和后缀最小值之类的后缀信息相关，长链剖分后合并短链的时候大于短链长度的部分可以直接继承，前面直接暴力做就行。

实现方法可以用指针数组实现，方便很多。

复杂度 \(O(n)\)。

CF2159 E. Super-Short-Polynomial-San

原题

给定多项式 \(g(x) = ax^2 + bx + c\)，定义 \(F(n)=g^n\)，\(q\) 次强制在线询问 \(\sum\limits_{j\le k_i} [x^j] F(n_i)\)。（不保证 \(n_i\) 的和，\(n_i \le 3\times 10^5\)）

假设 \(|F|>|G|\)， 求一个 \([x^k] F \cdot G\) 的复杂度只需要 \(O(|G|)\)，并且在得知 \(F\) 的前缀和的时候，求 \(\sum\limits_{j\le k} [x^j] F \cdot G\) 的时候也只需要 \(O(|G|)\)。

因此考虑类 BSGS 算法，按 \(B\) 分块，处理出 \(F(kB)\) 和 \(F(1)\ldots F(B)\)，后者可以直接暴力 \(O(B^2)\) 求出，前者直接倍增 FFT 可以做到 \(O(\dfrac{n^2\log n}{B})\)，回答询问可以做到 \(O(qB)\)，由于 \(n,q\) 同阶，复杂度为 \(O(n\sqrt{n\log n})\)，但由于需要三模 NTT，常数过大，无法通过。

考虑怎么快速求出一个 \(F(n)\)，由于 \(g\) 只是一个常数多项式，对于 \(g^n\) 类多项式，存在更快的计算方法：通过两种方法求出 \(F'(n+1)\)， \(F'(n+1)=((F(1))^{n+1})'=(F(1)\cdot F(n))'\)。展开后两项得，\(nF(n)\cdot F'(1)=F'(n)\cdot F(1)\)。把 \(F(n)\) 写成 \(\sum\limits_{i=0} p_i \cdot x^i\) 的形式，对比两边 \(x^i\) 项的系数，就可以求出 \(p_i\) 与 \(p_{i-k} \ldots p_{i-1}\) 之间的递推关系，其中 \(k\) 为 \(|g|\)，这里 \(k=2\)。那么就不需要 FFT，可以单次 \(O(n)\) 求出 \(F(n)\)。

所以最终的复杂度 \(O(n\sqrt{n})\)。

CF2159 F. Grand Finale: Snakes

原题

先把问题强化一下，求 \(n\) 个序列的问题。对于序列 \(i\)，考虑将其按长度为 \(i\) 分一块，开头在一个块里的区间里同时处理。观察这一块中区间的性质：左端点严格小于右端点，即加入的数不会被删。此时这个函数是单峰的，因为删数只会减小，加数只会上升，将两个单调的序列取 max，肯定是单峰的。

那么假如找到这 \(\sum\limits \lfloor \dfrac{n}{i} \rfloor = O(n\ln n)\) 个块的顶点，就相当于把这么多个有序序列做归并，每次取出最小值，把它所在的函数往一侧拓展一个位置即可。

考虑求这个函数的顶点，由于可能有相同的，所以不能直接二分判断 \(mid,mid+1\)，如果用 \(\log_{1.5} n\) 的三分，可能会爆。回归原问题，考虑当前的值是 \(t\)，那么当这条蛇走到 \(pos_t\) 的之前，值肯定不等于 \(t\)，那只需要问一下 假设 \(a_{i,j} = t\)，那么只需要问一下 \(i+j-2\) 时刻（也就是上一个时间）的值判断即可，次数是 \(2\log_{2} n\)。

总次数大约是 \(\Theta(n\log^2 n+m)\) 的，由于每次二分长度是 \(i\)，所以常数还会小一点，可以通过。

xsy2316B 挑战自动机(dfa)

原题

考虑暴力 bfs，每次暴力加入 \((x,y)\) 的后继状态，复杂度 \(O(n^2)\)。

考虑优化，若 \(x,y\) 等价，\(y,z\) 等价，那么 \(x,z\) 是等价的，即存在传递性（因为可以看成对于任意字符串都是相等的）。

那么若 \(x\neq z\)，则对于任意 \(y\)，有 \(x\neq y \lor y \neq z\)，所以当搜到状态 \((a,b),(b,c)\)，再加入一个 \((a,c)\) 时，\((a,c)\) 肯定不优于前两者之一，因为对于任意路径都会出现在前面两个中。

并且这个性质对于 \(>3\) 个数也肯定对的，所以加入状态时将其连边，每次只需要加不同连通块里的状态。由此可证答案 \(<n\)。

复杂度 \(O(n)\)。

xsy2339C 跳跃(jump) / xsy2316B 挑战自动机(dfa) 加强版

[原题]

考虑 dfa 最小化算法，那么 \((x,y)\) 的答案就是最小的字符串长度使得它们能被区分，也即在朴素 dfa 最小化算法中分裂的时间。

考虑修改 hopcroft 算法，记录每个等价类被分裂的时间并分层做。在朴素 hopcroft 算法中，当一个等价类被修改时若没有被当作证据使用过时，会将其分裂成两个小的证据，此时小的证据的时间会大于原来的，会导致错误更新其他的等价类。所以现在我们不将其分裂，只在队列中加入一个较小的证据即可，容易证明复杂度还是正确的。

复杂度 \(O((n+q)\log n \sum)\)

P14203 这次要永远 做朋友

原题

考虑 \(f(l+1,r) = t\) 的判断，设 \(s_i = 2pre_i - i\)，其中 \(pre_i\) 为 \(i\) 前缀 \(t\) 的出现次数，那么就是 \(s_r > s_l\)。

观察 \(s_i\) 有什么性质，若下一个数是 \(t\) 就加 \(1\)，否则减 \(1\)，可以发现当 \(t\) 出现次数较少时 \(s\) 是几乎单降的，于是可以猜测有用的点（存在 \(j>i \land s_j > s_i \lor j < i \land s_j < s_i\)）只有 \(O(cnt)\) 个，因为每次上升时只会影响多影响 \(O(1)\) 个点。进一步地，所有答案的区间并大小也只有 \(O(cnt)\)，因为每次插入一个点最多拓展 \(O(1)\) 位，所以也是对的。

枚举 \(f(l,r)\)，处理出这些有用的点（小于后缀最大值或大于前缀最小值），然后对每个区间先 \(O(n)\) 求出 mex 大于等于 \(t\) 的区间。令 \(R_i\) 为以 \(i\) 为左端点的最小右端点使得 mex \(\ge t\)，显然 \(R_i\) 是单调不降的，从左到右扫，每次若删掉的数 \(\le t\)，则将 \(R_{i+1} = \max(R_i,nxt_i)\)，否则就是 \(R_i\)。

然后考虑求答案，也就是求逆序对个数，由于相邻 \(s_i\) 的差不超过 \(1\)，所以在加入或删除点的时候有变化的个数也是 \(O(1)\)，直接双指针扫即可。

复杂度 \(O(n)\)。

P11420 [清华集训 2024] 乘积的期望

原题

设第 \(i\) 次操作选的位置是 \(pos_i\)，那么 \(a_i = \sum\limits_j [i - m < pos_j \le i] = \sum\limits_j [pos_j \le i] - \sum\limits_j [pos_j \le i - m]\)。答案即为 \(\prod\limits_i (\sum\limits_j [pos_j \le i] - \sum\limits_j [pos_j \le i - m])\)，把乘积拆开，相当于每个 \(i\) 选择一个 \(pos_j \le i\) 的，贡献为 \(1\)，或者选择一个 \(pos_j \le i - m\) 的，贡献为 \(-1\)。假设一共钦定了 \(num\) 个 \(j\)，概率是 \(ans_j\)，那么答案就是 \(\sum\limits_j \binom{c}{j} \cdot j! \cdot ans_j\)。

考虑设状态 \(f_{i,j,st}\) 为前 \(i\) 个数钦定了 \(j\) 个 \(pos\) 且 \(pos=i,i-1,\ldots,i-m+1\) 的个数集合是 \(st\)。由于 \(st\) 过大，但每个 \(i\) 只会匹配一个点，所以反过来去覆盖这个 \(i\)。改变 \(st\) 的定义为后 \(m\) 个数的覆盖状态，即这些数选择的是 \(-1\) 的贡献，在做到 \(i\) 时处理 \(i+m\)。当做到 \(i\) 且它没被覆盖时，就代表它选择了一个 \(1\) 的贡献，可以从 \(j\) 个中选一个或新开一个。

分析 \(st\) 的个数，由于 \(|st|\le2^m\)，且只有当 \(i \le n - m\) 的时候才会去覆盖后面的（将状态中添加一个 \(1\)），所以当 \(n \le 2m\) 的时候，\(n-m+1 \le i \le m\) 这些位置不可能被覆盖，所以是 \(O(2^{\min(m,n-m)} \cdot n^2)\)。

进一步地，当 \(n\ge 2m\) 时，最后 \(m\) 个位置实际上本质相同（选择 \(1\) 的贡献都是 \(n-m+1\) 之前的位置），因此没必要知道具体是哪些位置被覆盖，只用记录覆盖的个数。所以将序列分成前 \(n-2m\)，中间 \(m\) 和最后 \(m\) 三块。第一块用前面的转移，第二块的时候就不需要更新 st 了，状态加一维 \(f_{i,j,k,st}\) 表示覆盖了第三块的 \(k\) 个。第三块的时候直接钦定前 \(k\) 个为被覆盖，每次当 \(k>0\) 时强制 \(k\) 要减 \(1\) 即可。复杂度是 \(O(2^{\min(m,n-2m)} \cdot n^3)\)。

总复杂度为当 \(3m \le n\) 时，为 \(O(2^m \cdot n^2)\)，否则为 \(O(2^{\max(0,n-2m)} \cdot n^3)\)。

xsy2343D lemon

原题

对于平面图动态删边，可以转成对偶图的动态加边问题，两个点不连通相当于其中一个点在对偶图中被一个环包围在内了。（问一条边中的两个点联通情况：[AMPPZ2013] Bytehattan，可以直接判边的两边的对偶点是否联通。任意两点可以对偶点连边成环时启发式分裂原图的点）

在此题删一个点相当于是把四周的点连起来加四条边，合法相当于所有关键点在同一个极小环中。但是由于不一定真的断开，所以不能直接启发式分裂。

考虑判定，相当于对每个环 check 它包含的关键点集合是否是全集或空集，根据点在多边形内部的判定方法，我们将一个点引出一条任意向外的线（可以弯曲），若一个环被这条线穿过奇数次就包含这个点。

所以使用 xor-hash，把每个点的权值加到右边所有对偶图的边上。每次加边时，对新加的环 check 即可，可以使用带权并查集。由于合法的权值那么是固定的常数，要么是 \(0\)，所以只需 check 任意一个环合法，其他有交的必定合法。

复杂度 \(O(n\log n)\)。

P13305 [GCJ 2013 Finals] Can't Stop

原题

考虑暴力，从每个 \(l\) 出发往右搜索，若当前位置与集合交为空就枚举一个加入，复杂度 \(O(n^2 d^k)\)，多一个 \(n\) 是因为跳的过程。

考虑优化，在 \(l\) 开始搜的时候，我们不加入 \(l-1\) 位置的所有颜色，此操作显然不会影响答案，此时暴力跳的复杂度就是对的。原因是考虑从 \(r\) 往左搜的时候，在选了相同集合时

CF1874 F. Jellyfish and OEIS

原题

直接考虑原问题，会有诸如 \(i \to p_i\) 这些边覆盖整条 \([i, m_i]\) 类限制，很不好计数，所以考虑容斥。

枚举一个区间集合 \(S\)，对于每个集合中的区间 \([l,r]\)，将 \([l,r]\) 覆盖一种新的颜色，最后方案数是每种颜色集合的点个数阶乘的乘积，容斥系数为 \((-1)^{|S|}\)。

若直接 dp，无法考虑到每种颜色集合内的点并不连续的问题，区间 dp 也无法处理区间相交的情况。但是我们发现对于一种序列的覆盖的情况，会有多种 \(S\) 贡献到这个情况，这启发我们运用容斥系数抵消一些情况。

进一步地，当存在选择区间 \([l_1,r_1],[l_2,r_2]\) 满足 \(l_1 < l_2 \le r_1 < r_2\)，此时可以改变区间 \([l_1,l_2 - 1]\) 的选择情况，方案仍然相同。我们可以依此建立双射，对于一种这样的方案，找到最小的 \(i\) 使得其是一个 \(l_2 - 1\)，再找到满足交点是 \(i\) 最小的 \(l_1\)，是否选择 \([l_1,i]\) 之间形成双射。

那么就可以去掉相交的情况，可以直接区间 dp 了，容易设状态 \(f_{i,j,k}\) 表示区间 \([i,j]\) 有 \(k\) 个位置没被子区间覆盖，直接转移即可。

复杂度 \(O(n^4)\)。

CF1098 F. Ж-function

原题

先对原串翻转，建出 SAM，设前缀 \(i\) 在 SAM 的位置是 \(pos_i\)，要求的就是 \(\sum\limits_{i=l}^r \min(i-l+1,dep_{lca(pos_i, pos_r)})\)。

对后缀树重链剖分，把每个 \(i\) 和询问的 \(r\) 插到 \(pos_x\) 祖先的 \(O(\log n)\) 个重链中，对每个重链分别求答案，再减去来自同一轻子树的询问的前缀即可，那么现在就转成序列问题了。

为了方便，下设 \(dep_i\) 为 \(pos_i\) 在当前重链对应点的 dep。显然只需统计 \(dep_{lca} \le i - l + 1\) 的所有 \(dep_{lca}\) 之和与对应 \(i\) 之和，稍微讨论一下偏序关系容易得到询问 \([l,r]\) 的贡献：

• \(dep_i \le dep_r \land l \le i - dep_i + 1 \le i \le r\)。

• \(dep_i > dep_r \land l + dep_r - 1 \le i \le r\)。

第二个限制是好求的，但第一个限制是三维的限制，直接做需要两个 \(\log\)，比较劣。

观察到 \([i - dep_i + 1, i]\) 的区间长度刚好是 \(dep_i\)，此时不妨讨论一下与 \([l,r]\) 长度与 \(dep_r\) 的关系：

• 若 \(r - dep_r + 1 < l\)，此时 \(dep_i > dep_r\) 的 \(i\) 必定不会满足第一个限制，所以只用统计满足 \(l \le i - dep_i + 1 \le i \le r\) 的 \(i\) 即可。

• 若 \(r - dep_r + 1 \ge l\)，此时 \(dep_i \le dep_x\) 中不合法的 \(i\) 只需满足 \(i - dep_i + 1 < l\)，因为若 \(i>r\) 那么区间长度要大于 \(r - l + 1\)，就比 \(dep_r\) 大了。

此时通过讨论即可成功把限制降为二维的，bit 统计即可。

复杂度 \(O(n\log^2 n)\)。