机器学习算法基本型 分类（笔记）
数据工作逻辑
三个关键的误差水平
- 人类水平误差：假设，观察一张CT片子，不同的医生可能的误差是：普通医生误差10%，专家医生7%，一个专家组5%。这5%，就是现实世界的“最优可达到误差”的近似，也称为 “贝叶斯最优误差” 。理论上最低的误差，也不会低于这个值了；
- Avoidable bias（可避免偏差）：可避免偏差 = 训练集误差 - 人类水平误差。它衡量的是模型在训练集上相对于人类专家还差多少。这个值应该尽可能小，如果过大，就会欠拟合，需要通过对模型的调优（增加复杂度、调参数、训练再久一点等）来降低它；
- Variance（方差）： 方差 ≈ 测试集误差 - 训练集误差。它衡量的是模型从训练集到测试集的性能下降程度，这个值应该尽可能小，如果过大，就会过拟合。高方差意味着模型泛化能力差。
-
权衡关系：
-
降低偏差（可以让模型更复杂、加长模型训练时间、新的模型/算法）：通常会导致方差上升。
-
降低方差（可以简化模型、正则化、用更多的数据训练、数据调整/重新抽样、新的模型/算法）：通常会导致偏差上升。
-
我们的目标是找到最佳平衡点，使总误差最小。这种将avoidable bias和variance结合，就是机器学习领域的bias-variance trade-off（偏差-方差权衡）。一个很美好的目标是：误差小，偏差和方差也小，这是一个泛化能力很好的模型。实际中，误差、偏差、方差，多大是大呢，这个很难界定，但可以用经验做一些衡量。有这样一些经验，值得考虑：
-
- 如果方差 远大于 可避免偏差（至少3倍） → 先解决过拟合（减少模型复杂度、加正则化、获取更多数据等）；
- 如果可避免偏差 远大于 方差 （至少3倍）→ 先解决欠拟合（用更复杂的模型、训练更久等）
- 如果两者差不多 → 可以同时处理。
其次，还可以从开发误差是训练误差的几倍，判断是不是需要干预方差。以及业务要求的误差是多少，来决定是否要继续干预。
Tips：
1、贝叶斯最优误差：即使在拥有所有可能信息、做出最优决策的情况下，完成该任务仍然无法避免的最低错误率。它是由任务本身的模糊性决定的，而不是由学习者的能力决定的。比如上面的CT片子，可能由于图像质量、疾病本身的复杂性，或者信息的缺失，比如某些角度没拍到，导致这个任务本身具备一定的模糊性，你再提高自身能力，也一定会存在误差，这就是无法避免的错误。那和贝叶斯有什么关系呢？这是因为它的来源路径是：贝叶斯定理 → 贝叶斯分类器 → 贝叶斯最优误差。
1）从贝叶斯定理到最优分类器：以CT片子为例，根据这个片子，判断得癌症的概率，根据贝叶斯定理，可以基于“图像长成这样的概率（证据概率）“，以及“得癌症的概率（先验概率）“和“如果得癌症，我会有这种图像的概率（似然概率）”，得到得癌症的后验概率。即
P(癌症 | x) = [P(x | 癌症) × P(癌症)] / P(x)
= (0.3 × 0.01) / 0.031
≈ 0.003 / 0.031
≈ 0.0968 ≈ 9.7%
那么：P(正常 | x) = 1 - P(癌症 | x) ≈ 90.3%
此时，假设有一个全知全能的“上帝诊断系统”，它知道所有可能的概率，那它做决策，肯定是选择概率大的那个。比如，如果 P(癌症 | x) > P(正常 | x) → 预测癌症，否则 → 预测正常。上面的例子里，P(癌症 | x) ≈ 9.7%，P(正常 | x) ≈ 90.3%，9.7% < 90.3%，所以，在这种图像下，就可以判断，你没病，正常。那么问题就是，你没有上帝视角，你并不知道P(x | 癌症) ，也不知道P(癌症)、P(x)，这三个数据，本身的获取，存在误差。贝叶斯最优分类的意义主要在于，我假定你就是准确的概率结果，那我会怎么做决策，我的决策思路就是，谁概率大我选谁。它其实也隐藏了一个含义：如果你的估计足够准确，那你基于贝叶斯分类器大概率得到正确的决策（因为后验概率也不是100%，我只是让你选择错误率低的那个，也就是（1-后验概率）小的）。如果你概率就是错的，那根据我的分类器，你决策错了，这也不是我导致的决策误差。
2）从贝叶斯最优分类器到贝叶斯最优误差：理论上的贝叶斯最优分类器在实际应用时会犯的错误率。也就是P(error∣x)=1−max{P(C=1∣x),P(C=0∣x)}，选择了最大的那个概率，仍然可能犯错的概率。为了方便使用，通常使用P(error∣x)=min{P(C=1∣x),P(C=0∣x)}。然后把每个x对应的错误率，乘上x出现的概率，全部相加求平均，得到对应的错误率， 求平均，就是贝叶斯最优误差。比如：
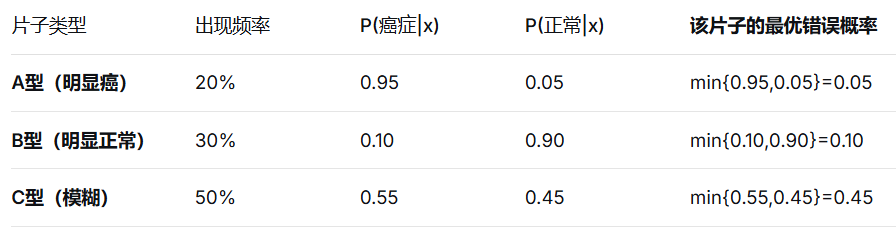
那么，总最优误差 = (A型出现频率 × A型最优错误概率) + (B型出现频率 × B型最优错误概率) + (C型出现频率 × C型最优错误概率)
= (20% × 0.05) + (30% × 0.10) + (50% × 0.45)
= 0.01 + 0.03 + 0.225
= 0.265 = 26.5%
这个26.5%就是贝叶斯最优误差。
2、方差，数学上不是用来做稳定性的判断么？这里为什么又用来做误差的判断了呢？其实这是因为 期望误差=偏差²+方差+σ²，方差项确实会导致测试误差上升，高方差的模型必然在测试集上表现更差。既然，我能轻易算：测试误差 - 训练误差，那我就用“测试误差 - 训练误差”来代表“期望误差”吧。而期望误差，又和方差强相关。于是大家开始用“方差”指代“泛化差距”。可以理解为这是“方差”这个术语，在机器学习上的一个演化叫法。
效果指标
- TP（True Positive）：被判定为正样本，且事实上也是正样本
- FP（False Positive）：被判定为正样本，但事实上是负样本（误报）
- TN（True Negative）：被判定为负样本，且事实上也是负样本
- FN（False Negative）：被判定为负样本，但事实上是正样本（漏报）
构造混淆矩阵：
- Precision：查准率 （即在检索后返回的结果中，正确个数占整个结果的比例。强调正确率。），precision = TP/(TP+FP)；
- Recall：查全率 （即在检索结果中真正正确的个数 占整个数据集（检索到的和未检索到的）中真正正确个数的比例。强调是否有漏报。），recall = TP/(TP+FN)；
- F-Measure/ F-Score ：Precision和Recall平均 （P和R指标有时候会出现矛盾），用这个值来帮助进一步判断。
分类算法-决策树
熵的单位是比特（bit），因为公式里用的是 log2，代表是二进制，二进制单位是bit.为什么用log2就代表是二进制？因为假设用二进制编码，码长 L 位。每增加 1 位，可能性数量乘以 2（因为每位有 2 种选择）。总可能性数量，就是2的L次方。如果现在我需要N种可能，也就是需要
，那么 
。这个L就是码长，也就是几位二进制。比如8种可能性，就是2³，也就是L=log28=3，二进制的码长或者说二进制的位数，就是3bit，也就是用3位来表示8种，000,001,010,011... ...
所以，这个公式可以看出来，求熵，就是求它平均使用了多少比特/多少码字长度。更进一步的理解，当你使用了更多的比特(对应码子长度高)，那么代表你输入了更多的限制条件或者影响条件或者可能性，也就因此，不确定性更高。
2、二元系统计算等概率事件的熵，为啥为log2 2=1比特？
当N=2时，就是log22=1。如果N=3时（有3个结果），那就是log23，大概是1.585 比特.
构造树的基本想法是，随着树深度的增加，节点的熵迅速降低，来让我们更高效地确定一个事情。如何刻画这个降低效率？方法是，用前后两次的熵相减，值越大，说明新的规则熵越小，相对来说它本身的确定性就大，那么因此带来的确定性就大，也就是选择它以后，价值更大，可以更快得到有效结果。这个差值，就是信息增益Gain（S,A）,S是基于的基本环境，A是要计算的目标环境。以下面的天气示例，来进行说明：
1、确认根节点。
1）确认初始熵：在没有天气状况、温度、湿度、风力这些信息的情况下，直接根据14天的打球结果，计算初始熵。这14天，去打球是9天，不打球是5天，所以打球概率是9/14，不打球概率是5/14，代入信息熵的公式，计算初始熵；
2）分别计算四种情况的信息熵，以及对应的信息增益：
a 如果知道了天气，那么打球结果是什么情况的信息熵、信息增益；
b 如果知道了温度，那么打球结果是什么情况的信息熵、信息增益；
c 如果知道了湿度，那么打球结果是什么情况的信息熵、信息增益；
d 如果知道了风力，那么打球结果是什么情况的信息熵、信息增益。
具体计算如下：
a 如果知道了天气，那么打球结果是什么情况的信息熵、信息增益：
1）计算晴朗时，打球的熵。晴朗时，一共是5天，2天打球，3天不打球。所以晴朗时，打球概率2/5，不打球概率3/5。代入信息熵的公式，得到0.97比特；
2）计算阴天时，打球的熵。阴天全部选择打球，因为只有这一种可能，所以信息熵最小，为0；
3）计算雨天时，打球的熵。雨天时，一共是5天，3天打球，2天不打球。所以雨天时，打球概率3/5，不打球概率2/5。代入信息熵的公式，得到0.97比特；
4）因此，在天气的影响下，是否打球的整体熵，需要结合这三种情况，并分别*对应天气发生的概率，作为权重，得到整体熵的结果。比如14天里，5天晴朗，4天阴天，5天下雨，整体熵=5/14*0.97+4/14*0+5/14*0.97=0.693；
5）天气的信息增益=初始熵-天气熵=0.94-0.693=0.247.
b 如果知道了温度，那么打球结果是什么情况的信息熵、信息增益---同理计算得到，Gain（温度）=0.029；
c 如果知道了湿度，那么打球结果是什么情况的信息熵、信息增益---同理计算得到，Gain（湿度）=0.152；
d 如果知道了风力，那么打球结果是什么情况的信息熵、信息增益---同理计算得到，Gain（风力）=0.048.
综上，四种情况里面，Gain（天气）是最大的，所以根节点选择天气。
2、根节点为天气，那么会有三个分支：晴朗、阴天、雨天。那么每个分支下面，应该选择什么节点呢？
1)以晴朗分支开始计算，在基于晴朗的前提下，分别计算如下几种情况的信息熵和信息增益。这里的初始熵，为晴朗天气的熵，上面已经计算过，为0.97：
a 晴朗天气下，如果知道了温度 ，那么打球结果是什么情况的信息熵、信息增益；
b 晴朗天气下，如果知道了湿度 ，那么打球结果是什么情况的信息熵、信息增益；
c 晴朗天气下，如果知道了风力 ，那么打球结果是什么情况的信息熵、信息增益。
具体计算如下：
a 晴朗天气下，如果知道了温度 ，那么打球结果是什么情况的信息增益：
1）晴朗天气一共5天，对应着hot是是2天（2/5），mild是2天（2/5），cool是1天（1/5）；
2）晴朗天气下，hot打球全部是no，熵为0；mild打球一天去，一天不去，熵为1；cool打球全部是去，熵为0；
3）这里的初始熵，为晴朗天气的熵，上面已经计算过，为0.97。因此晴朗天气下，温度的信息增益计算如下：
使用weka练习一个分类算法-cars
实验目的：通过构建J48决策树分类模型，对汽车购买推荐进行预测分析。具体包括： 探索影响汽车购买决策的关键因素（即根节点和高层节点）、验证模型的泛化能力和实际应用价值（采用训练集-测试集分离验证的方式。通过对训练集进行训练，得到模型，然后在测试集上进行验证，结果和测试集的真实结果进行对比，得到混淆矩阵，了解模型的应用价值）。
数据说明：数据集的属性包括buying（价格低、中、高、很高）、maint（维护）、doors（几扇门）、persons（乘载几人）、lug_boot（后备箱多大）、safety（安全系数）、CAR（只有0和1，代表不购买和购买）。
实验步骤：
1、训练阶段：用训练集（1209条）建立J48决策树模型
2、预测阶段：用建好的模型对测试集（519条）进行预测
3、评估阶段：运行结果如下。通过对预测结果与测试集真实的CAR标签进行比对，得到混淆矩阵，进而得到精准度等指标，判断此模型的应用价值
正为1，购买；负为0，不购买。
J48常用参数的说明：
指标的说明：
- kappa：(观察一致性 - 期望一致性) / (1 - 期望一致性)。其中，观察一致性可以理解为准确率，即（预测为0，实际为0+预测为1，实际为1），在所有测试集的占比；期望一致性，需要先计算出实际结果为0、1的概率，预测结果为0、1的概率。假设预测、实际都是独立随机事件，所以整体随机猜中0的概率就是（实际0的概率*预测0的概率），整体随机猜中1的概率就是（实际1的概率*预测1的概率），两者相加，为整体期望一致性
- 混淆矩阵：根据截图中红色字体的说明，建立矩阵。进而涉及4个关键数据：TP（预测为1，实际为1）、TN（预测为0，实际为0）、FP（预测为1，实际为0）、FN（预测为0，实际为1）。Precision = TP/(TP+FP)，即预测为正的样本中，真正为正的比例
其他
如果想看这棵树的整体效果，可以右键运行结果标题，选择visualize tree。之后点击 fit to screen，就可以看到清晰的树结构了。
可以看到，根节点是safety，说明客户购买的最主要参考因素，就是安全性，安全性为1的，全部不购买。接下来是考虑坐几个人，再来是考虑价格。
实验小结：此模型的泛化能力在本数据集上表现很好，准确度达到了96%.kappa值0.916，也说明模型预测结果与真实结果的一致性很高，并不是随机猜对的。可以用于预测客户购买的决策（首先是考虑安全性，其次是载客量，再来是价格），也可以考虑利用在二手车价值的评判、保险风险评估的评判上。
本文来自博客园，作者：1234roro 当你迷惘的时候，开始学习吧！当你目标清晰的时候，开始学习吧！转载请注明原文链接：https://chuna2.787528.xyz/1234roro/p/19487269
浙公网安备 33010602011771号